
Cho chóp tứ giác \(S.ABCD\) có đáy là hình chữ nhật với \(AB = 4a,\) \(AD = 3a\). Các cạnh bên đều có độ dài \(5a\). Góc nhị diện \(\left[ {S,BC,A} \right]\) có số đo là
A. \({75^ \circ }46’\).
B. \({71^ \circ }21’\).
C. \({68^ \circ }31’\).
D. \({65^ \circ }12’\).

Cách xác định góc nhị diện \(\left[ {{P_1},d,{Q_1}} \right]\)
Bước 1: Xác định \(c = \left( {{P_1}} \right) \cap \left( {{Q_1}} \right)\).
Bước 2: Tìm mặt phẳng \(\left( R \right) \supset c\).
Bước 3: Tìm \(p = \left( R \right) \cap \left( {{P_1}} \right),q = \left( R \right) \cap \left( {{Q_1}} \right),O = p \cap q,M \in p,N \in q\).
Advertisements (Quảng cáo)
Khi đó \(\left[ {{P_1},d,{Q_1}} \right] = \widehat {MON}\).

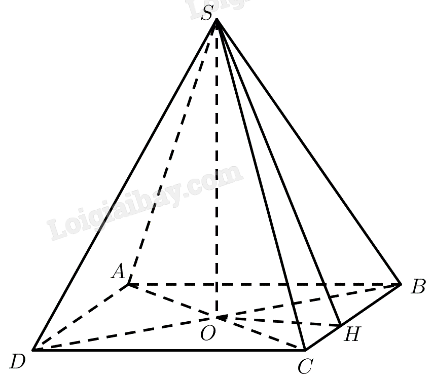
Gọi \(O\) là tâm của đáy. Kẻ \(OH \bot BC\left( {H \in BC} \right)\).
\(\Delta SAC\) cân tại \(S\)\( \Rightarrow SO \bot AC\)
\(\Delta SB{\rm{D}}\) cân tại \(S\)\( \Rightarrow SO \bot B{\rm{D}}\)
\( \Rightarrow SO \bot \left( {ABCD} \right) \Rightarrow SO \bot BC\)
Mà \(OH \bot BC\)
Vậy \(\widehat {SHO}\) là góc nhị diện \(\left[ {S,BC,A} \right]\).
\(\begin{array}{l}{S_{ABC{\rm{D}}}} = AB.A{\rm{D}} = 12{a^2} \Rightarrow {S_{OBC}} = \frac{1}{4}{S_{ABC{\rm{D}}}} = 3{a^2}\\{S_{OBC}} = \frac{1}{2}BC.OH \Rightarrow OH = \frac{{2{{\rm{S}}_{OBC}}}}{{BC}} = 2a\\AC = \sqrt {A{B^2} + B{C^2}} = 5a \Rightarrow OC = \frac{1}{2}AC = \frac{{5a}}{2}\\SO = \sqrt {S{C^2} - O{C^2}} = \frac{{5a\sqrt 3 }}{2}\\\tan \widehat {SHO} = \frac{{SO}}{{OH}} = \frac{{5\sqrt 3 }}{4} \Rightarrow \widehat {SHO} \approx {65^ \circ }12’\end{array}\)
Chọn D.
