
Khi đu quay hoạt động, vận tốc theo phương ngang của một cabin M phụ thuộc vào góc lượng giác \(\alpha \; = \;(Ox,OM)\)theo hàm số \({v_x} = 0,3sin\alpha \;\) (m/s) (Hình 11).
a) Tìm giá trị lớn nhất và giá trị nhỏ nhất của \({v_x}\)
b) Dựa vào đồ thị của hàm số sin, hãy cho biết trong vòng quay đầu tiên \((0 \le \alpha \le 2\alpha )\), góc \(\alpha \)ở trong các khoảng nào thì \({v_x}\) tăng.
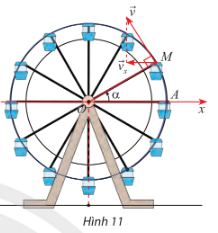

Dựa vào hình vẽ và sử dụng đồ thị hàm số sin để trả lời.
Advertisements (Quảng cáo)

a) Do \( - 1 \le sin\alpha \le 1\;\)nên \( - 0,3 \le sin\alpha \le 0,3\)
Vậy giá trị lớn nhất của \({v_x}\) là 0,3 (m) và giá trị nhỏ nhất của \({v_x}\) là -0,3 (m).
b) Ta có đồ thị hàm số:
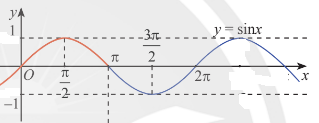
Với góc \(\alpha \in \left( {0;\frac{\pi }{2}} \right)\) hoặc \(\alpha \in \left( {\frac{{3\pi }}{2};2\pi } \right)\) thì \({v_x}\) tăng.
