
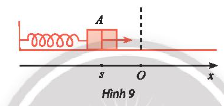
Trong Hình 9, khi được kéo ra khỏi vị trí cân bằng ở điểm O và buông tay, lực đàn hồi của lò xo khiến vật A gắn ở đầu của lò xo dao động quanh O. Toạ độ s (cm) của A trên trục Ox vào thời điểm t (giây) sau khi buông tay được xác định bởi công thức \(s = 10sin\left( {10t + \frac{\pi }{2}} \right).\)Vào các thời điểm nào thì \(s = - 5\sqrt 3 \;\)cm?

Phương trình sinx = m ,
- Nếu \(\left| m \right| \le 1\) thì phương trình vô nghiệm.
- Nếu \(\left| m \right| \le 1\) thì phương trình có nghiệm:
Khi đó, tồn tại duy nhất \(\alpha \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) thoả mãn \(\sin \alpha = m\),
Advertisements (Quảng cáo)
\({\mathop{\rm s}\nolimits} {\rm{inx}} = m \Leftrightarrow \sin x = \sin \alpha \)\( \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi - \alpha + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)

Khi: \(s = - 5\sqrt 3 \;\)thì \(10sin\left( {10t + \frac{\pi }{2}} \right) = - 5\sqrt 3 \; \Leftrightarrow sin\left( {10t + \frac{\pi }{2}} \right) = - \frac{{\sqrt 3 }}{2}\)
\(\begin{array}{l} \Leftrightarrow sin\left( {10t + \frac{\pi }{2}} \right) = \sin \left( { - \frac{\pi }{3}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}10t + \frac{\pi }{2} = - \frac{\pi }{3} + k2\pi \\10t + \frac{\pi }{2} = \pi + \frac{\pi }{3} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t = - \frac{\pi }{{12}} + k\frac{\pi }{5}\\t = \frac{\pi }{{12}} + k\frac{\pi }{5}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
Vậy \(t = \pm \frac{\pi }{{12}} + k\frac{\pi }{5},k \in \mathbb{Z}\) là giá trị cần tìm.
