Hoạt động 2
a) Có giá trị nào của x để \(sinx = 1,5\)không?
b) Trong Hình 1, những điểm nào trên đường tròn lượng giác biểu diễn góc lượng giác x có \(sinx = 0,5\)? Xác định số đo của các góc lượng giác đó.
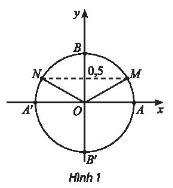

Quan sát hình và dựa vào tính chất \( - 1 \le sinx \le 1\).

a) Với mọi \(x \in \mathbb{R}\), ta có: \( - 1 \le sinx \le 1\)
Do đó không có giá trị nào của x để \(sinx = 1,5\).
b) Những điểm biểu diễn góc lượng giác có \(sinx = 0,5\) là M và N.
Điểm M biểu diễn cho các góc lượng giác có số đo là \(\frac{\pi }{6} + k2\pi ,k \in \mathbb{Z}.\)
Điểm N biểu diễn cho các góc lượng giác có số đo là \(\frac{{5\pi }}{6} + k2\pi ,k \in \mathbb{Z}.\)
Advertisements (Quảng cáo)
Thực hành 2
Giải các phương trình sau:
\(\begin{array}{l}a)\;sinx = \frac{{\sqrt 3 }}{2}\\b)\;sin(x + {30^o}) = sin(x + {60^o})\end{array}\)

Nếu \(\left| m \right| \le 1\) thì phương trình:
- \({\mathop{\rm s}\nolimits} {\rm{inx}} = m \Leftrightarrow \sin x = \sin \alpha \)\( \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi - \alpha + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
- \(\sin x = \sin {\alpha ^o} \Leftrightarrow \left[ \begin{array}{l}x = {\alpha ^o} + k{360^o}\\x = {180^o} - {\alpha ^o} + k{360^o}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\)

\(a)\;sinx = \frac{{\sqrt 3 }}{2}\)
Vì \(sin\frac{\pi }{3} = \frac{{\sqrt 3 }}{2}\) nên \(sinx = \frac{{\sqrt 3 }}{2} \Leftrightarrow sin\frac{\pi }{3} = sin\frac{\pi }{3}\) \( \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{3} + k2\pi ,k \in \mathbb{Z}\\x = \pi - \frac{\pi }{3} + k2\pi ,k \in \mathbb{Z}\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{3} + k2\pi ,k \in \mathbb{Z}\\x = \frac{{2\pi }}{3} + k2\pi ,k \in \mathbb{Z}\end{array} \right.\)
Vậy phương trình có nghiệm là \(x = \frac{\pi }{3} + k2\pi \) hoặc \(x = \frac{{2\pi }}{3} + k2\pi \)\(,k \in \mathbb{Z}\).
\(\begin{array}{l}b)\;sin(x + {30^o}) = sin(x + {60^o})\\ \Leftrightarrow \left[ \begin{array}{l}x + {30^o} = x + {60^o} + k{360^o},k \in \mathbb{Z}\\x + {30^o} = {180^o} - x - {60^o} + k{360^o},k \in \mathbb{Z}\end{array} \right.\\ \Leftrightarrow x = {45^o} + k{180^o},k \in \mathbb{Z}.\end{array}\)
Vậy phương trình có nghiệm là \(x = {45^o} + k{180^o},k \in \mathbb{Z}\).
