Hoạt động 2
Từ một điểm \(O\) vẽ hai tia \(Ox\) và \(Oy\) lần lượt vuông góc với hai bức tường trong phòng. Đo góc \(xOy\).
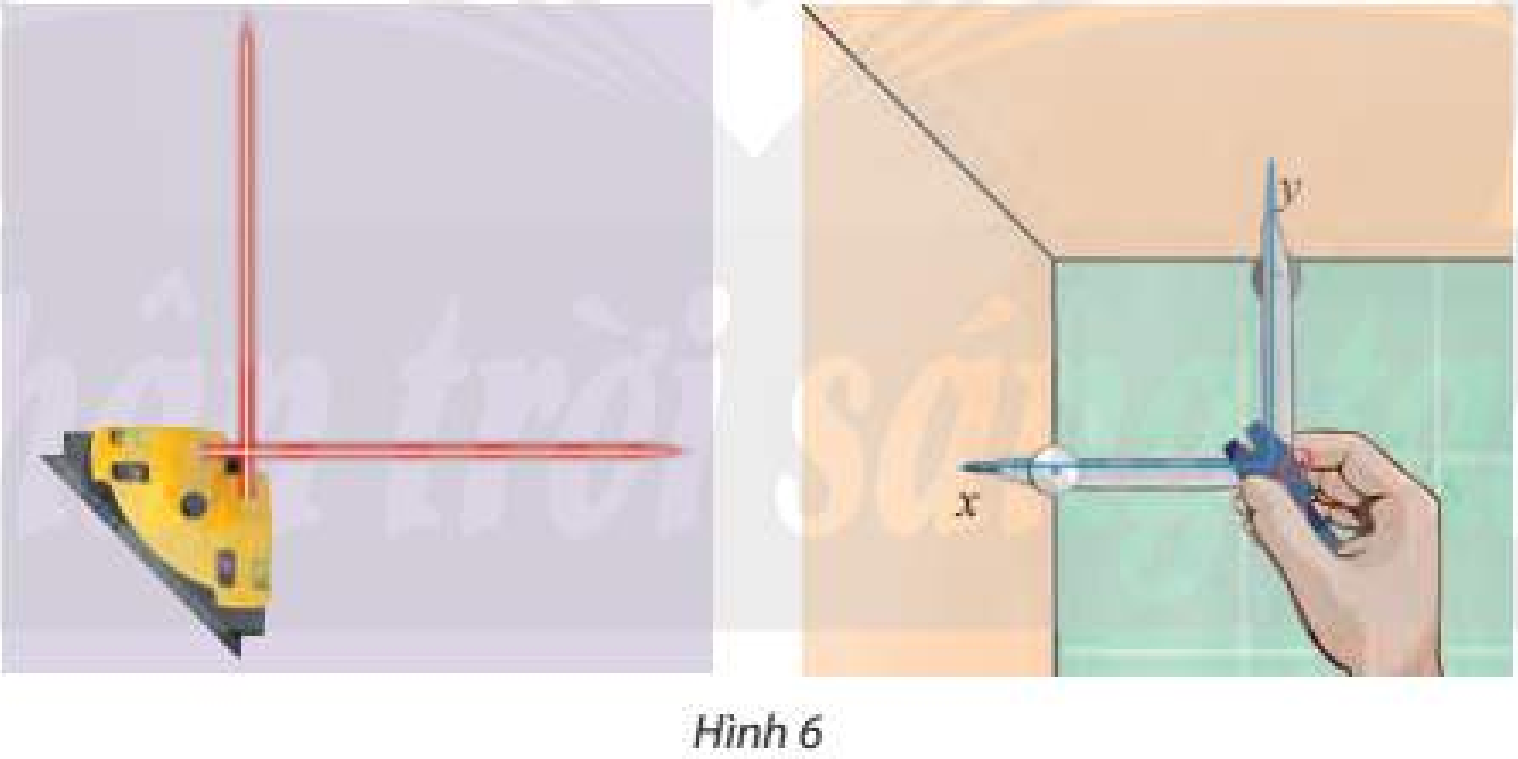

Thực hành đo góc và trả lời câu hỏi.

\(\widehat {xOy} = {90^ \circ }\).
Hoạt động 3
Cho hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) cắt nhau theo giao tuyến \(d\) điểm \(M\) không thuộc \(\left( P \right)\) và \(\left( Q \right)\). Gọi \(H\) và \(K\) lần lượt là hình chiếu vuông góc của \(M\) lên \(\left( P \right)\) và \(\left( Q \right)\). Gọi \(O\) là giao điểm của \(d\) và \(\left( {MHK} \right)\) (Hình 8).

a) Giả sử \(\left( P \right) \bot \left( Q \right)\), hãy cho biết tứ giác \(MHOK\) là hình gì? Tìm trong \(\left( P \right)\) đường thẳng vuông góc với \(\left( Q \right)\).
b) Giả sử \(\left( P \right)\) chứa đường thẳng \(a\) với \(a \bot \left( Q \right)\), hãy cho biết tứ giác \(MHOK\) là hình gì? Tính góc giữa \(\left( P \right)\) và \(\left( Q \right)\).

Sử dụng định nghĩa: Góc giữa hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) là góc giữa hai đường thẳng lần lượt vuông góc với \(\left( \alpha \right)\) và \(\left( \beta \right)\).

a) Ta có:
\(\begin{array}{l}MH \bot \left( P \right) \Rightarrow MH \bot OH\\MK \bot \left( Q \right) \Rightarrow MK \bot OK\\\left( {\left( P \right),\left( Q \right)} \right) = {90^ \circ } \Rightarrow \left( {MH,MK} \right) = {90^ \circ } \Rightarrow MH \bot MK\end{array}\)
Tứ giác \(MHOK\) có \(\widehat {MHO} = \widehat {MK{\rm{O}}} = \widehat {HMK} = {90^ \circ }\).
Vậy tứ giác \(MHOK\) là hình chữ nhật.
Trong \(\left( P \right)\) có đường thẳng \(OH\) vuông góc với \(\left( Q \right)\).
b) Ta có:
\(\left. \begin{array}{l}a \bot \left( Q \right) \Rightarrow a \bot OK\\MH \bot \left( P \right) \Rightarrow MH \bot a\end{array} \right\} \Rightarrow MH\parallel OK\)
Lại có \(MH \bot \left( P \right)\). Vậy \(OK \bot \left( P \right) \Rightarrow OK \bot OH\)
Tứ giác \(MHOK\) có \(\widehat {MHO} = \widehat {MK{\rm{O}}} = \widehat {HOK} = {90^ \circ }\).
Vậy tứ giác \(MHOK\) là hình chữ nhật.
Advertisements (Quảng cáo)
\(\left( {\left( P \right),\left( Q \right)} \right) = \left( {MH,MK} \right) = \widehat {HMK} = {90^ \circ }\).
Thực hành 1
Cho hình chóp \(S.ABCD\) có các cạnh bên bằng nhau và đáy là hình vuông. Chứng minh rằng:
a) \(\left( {SAC} \right) \bot \left( {ABCD} \right)\);
b) \(\left( {SAC} \right) \bot \left( {SBD} \right)\).

Cách chứng minh hai mặt phẳng vuông góc: chứng minh mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng.

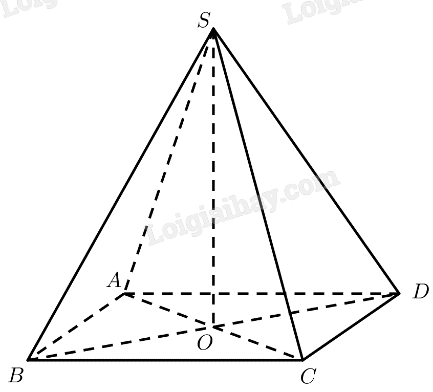
a) Gọi \(O = AC \cap B{\rm{D}}\).
Tam giác \(SAC\) cân tại \(S \Rightarrow SO \bot AC\)
Tam giác \(SB{\rm{D}}\) cân tại \(S \Rightarrow SO \bot B{\rm{D}}\)
\(\left. \begin{array}{l} \Rightarrow SO \bot \left( {ABCD} \right)\\SO \subset \left( {SAC} \right)\end{array} \right\} \Rightarrow \left( {SAC} \right) \bot \left( {ABCD} \right)\)
b) \(ABCD\) là hình vuông \( \Rightarrow AC \bot B{\rm{D}}\)
\(SO \bot AC\)
\(\left. \begin{array}{l} \Rightarrow AC \bot \left( {SB{\rm{D}}} \right)\\AC \subset \left( {SAC} \right)\end{array} \right\} \Rightarrow \left( {SAC} \right) \bot \left( {SB{\rm{D}}} \right)\)
Vận dụng 1
Mô tả cách kiểm tra một bức tường vuông góc với mặt sàn bằng hai cái êke trong Hình 10.
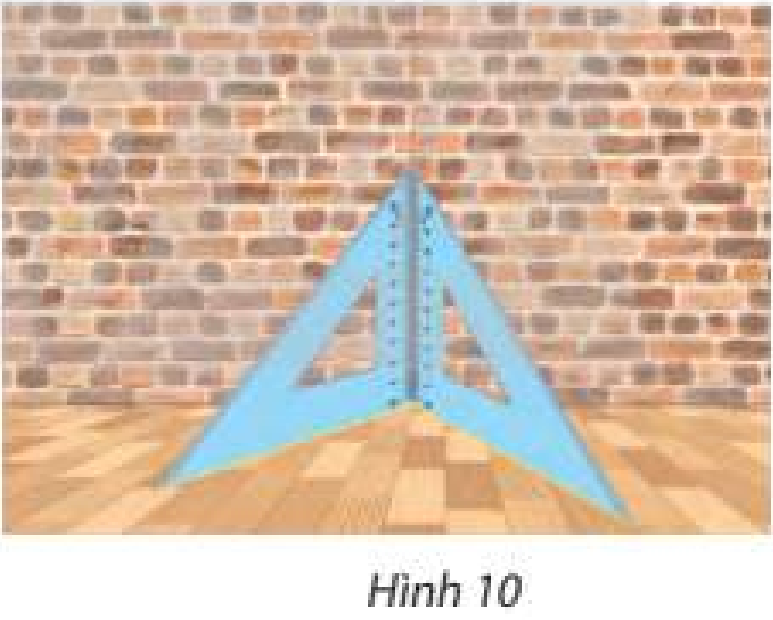

Sử dụng định lí 1: Điều kiện cần và đủ để hai mặt phẳng vuông góc là mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.

Đặt êke sao cho hai cạnh góc vuông của hai êke chạm nhau tạo thành một đường thẳng, hai cạnh còn lại của hai êke sát với mặt sàn.
Nếu đường thẳng đó nằm sát với bức tường thì bức tường vuông góc với mặt sàn.
