Hoạt động 4
Cho đường thẳng \(a\) vuông góc với mặt phẳng \(\left( Q \right)\). Mặt phẳng \(\left( P \right)\) chứa \(a\) và cắt \(\left( Q \right)\) theo giao tuyến \(c\). Trong \(\left( Q \right)\) ta vẽ đường thẳng \(b\) vuông góc với \(c\).
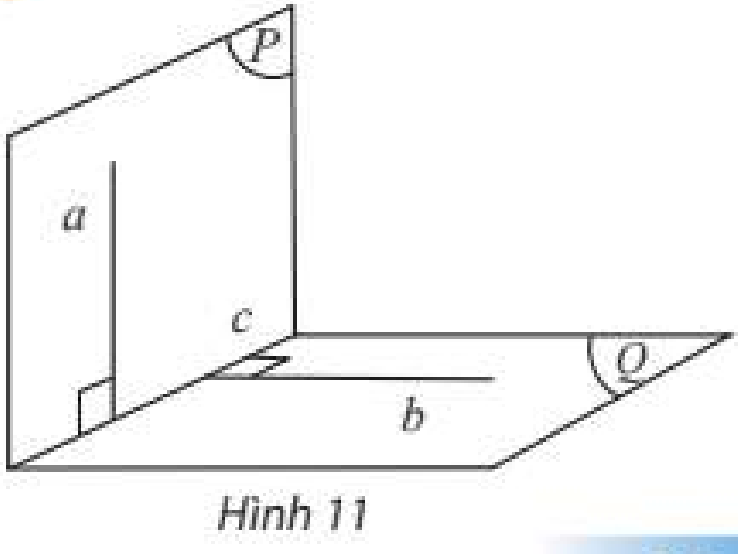
Hỏi:
a) \(\left( P \right)\) có vuông góc với \(\left( Q \right)\) không?
b) Đường thẳng \(b\) vuông góc với \(\left( P \right)\) không?

Sử dụng định lí 1: Điều kiện cần và đủ để hai mặt phẳng vuông góc là mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.

a) Ta có:
\(\left. \begin{array}{l}a \bot \left( Q \right)\\a \subset \left( P \right)\end{array} \right\} \Rightarrow \left( P \right) \bot \left( Q \right)\)
b) Ta có:
\(\left. \begin{array}{l}\left. \begin{array}{l}a \bot \left( Q \right)\\b \subset \left( Q \right)\end{array} \right\} \Rightarrow a \bot b\\b \bot c\\a,c \subset \left( P \right)\end{array} \right\} \Rightarrow b \bot \left( P \right)\)
Hoạt động 5
Cho hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) cùng vuông góc với mặt phẳng \(\left( R \right)\). Gọi \(a\) là giao tuyến của \(\left( P \right)\) và \(\left( Q \right)\). Lấy điểm \(M\) trong \(\left( R \right)\), vẽ hai đường thẳng \(MH\) và \(MK\) lần lượt vuông góc với \(\left( P \right)\) và \(\left( Q \right)\). Hỏi:
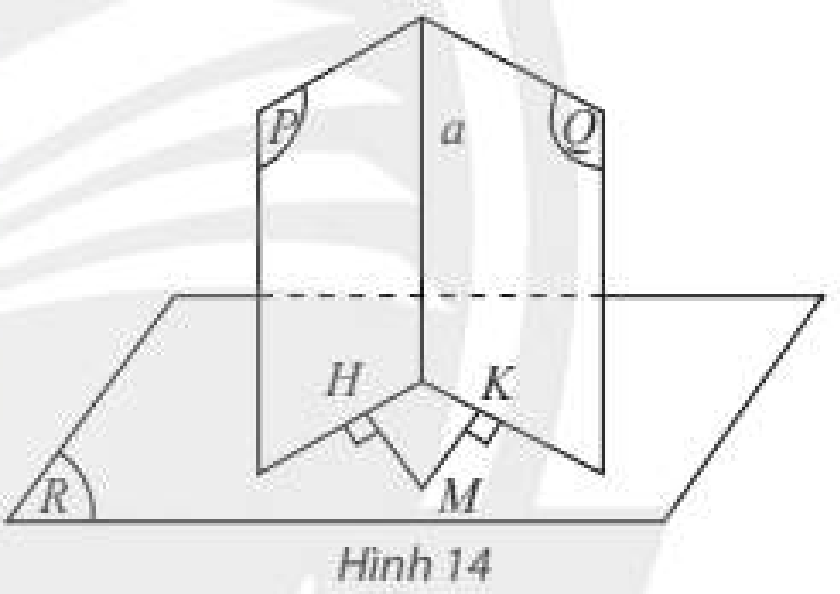
a) Hai đường thẳng \(MH\) và \(MK\) có nằm trong \(\left( R \right)\) không?
b) Đường thẳng \(a\) có vuông góc với \(\left( R \right)\) không?

Sử dụng định lí 1: Điều kiện cần và đủ để hai mặt phẳng vuông góc là mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.

a) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}M \in \left( R \right)\\MH \bot \left( P \right)\\\left( R \right) \bot \left( P \right)\end{array} \right\} \Rightarrow MH \subset \left( R \right)\\\left. \begin{array}{l}M \in \left( R \right)\\MK \bot \left( Q \right)\\\left( R \right) \bot \left( Q \right)\end{array} \right\} \Rightarrow MK \subset \left( R \right)\end{array}\)
b) Ta có:
\(\left. \begin{array}{l}MH \bot \left( P \right) \Rightarrow MH \bot a\\MK \bot \left( Q \right) \Rightarrow MK \bot a\\MH,MK \subset \left( R \right)\end{array} \right\} \Rightarrow a \bot \left( R \right)\)
Thực hành 2
Advertisements (Quảng cáo)
Tứ diện \(ABCD\) có \(AB \bot \left( {BCD} \right)\). Trong tam giác \(BCD\) vẽ đường cao \(BE\) và \(DF\) cắt nhau tại \(O\). Trong mặt phẳng \(\left( {ACD} \right)\) vẽ \({\rm{D}}K\) vuông góc với \(AC\) tại \(K\). Gọi \(H\) là trực tâm của tam giác \(ACD\). Chứng minh rằng:
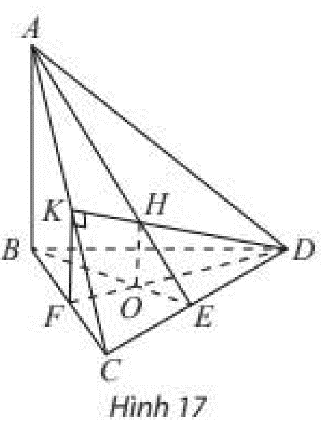
a) \(\left( {ADC} \right) \bot \left( {ABE} \right)\) và \(\left( {ADC} \right) \bot \left( {DFK} \right)\);
b) \(OH \bot \left( {ADC} \right)\).

‒ Cách chứng minh hai mặt phẳng vuông góc: chứng minh mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng.
‒ Cách chứng minh đường thẳng vuông góc với mặt phẳng:
+ Cách 1: chứng minh đường thẳng đó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng.
+ Cách 2: sử dụng định lí: Nếu hai mặt phẳng cắt nhau cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba.

a) Ta có:
\(\left. \begin{array}{l}AB \bot \left( {BC{\rm{D}}} \right) \Rightarrow AB \bot C{\rm{D}}\\BE \bot CE\end{array} \right\} \Rightarrow C{\rm{D}} \bot \left( {ABE} \right)\)
Lại có \(C{\rm{D}} \subset \left( {A{\rm{D}}C} \right)\)
Vậy \(\left( {ADC} \right) \bot \left( {ABE} \right)\)
\(\begin{array}{l}\left. \begin{array}{l}AB \bot \left( {BC{\rm{D}}} \right) \Rightarrow AB \bot DF\\DF \bot BC\end{array} \right\} \Rightarrow DF \bot \left( {ABC} \right)\\\left. \begin{array}{l} \Rightarrow DF \bot AC\\DK \bot AC\end{array} \right\} \Rightarrow AC \bot \left( {DFK} \right)\end{array}\)
Lại có \(AC \subset \left( {A{\rm{D}}C} \right)\)
Vậy \(\left( {ADC} \right) \bot \left( {DFK} \right)\)
b) Ta có:
\(\left. \begin{array}{l}\left( {ADC} \right) \bot \left( {ABE} \right)\\\left( {ADC} \right) \bot \left( {DFK} \right)\\\left( {ABE} \right) \cap \left( {DFK} \right) = OH\end{array} \right\} \Rightarrow OH \bot \left( {ADC} \right)\)
Vận dụng 2
Nêu cách đặt một quyển sách lên mặt bàn sao cho tất cả các trang sách đều vuông góc với mặt bàn.

Sử dụng định lí: Nếu hai mặt phẳng cắt nhau cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba.

Ta mở quyển sách ra và đặt quyển sách lên mặt bàn sao cho hai mép dưới của bìa sách nằm trên mặt bàn.
