
Một thấu kính hội tụ có tiêu cự f= 30 cm. Trong Vật lí, ta biết rằng nếu đặt vật thật AB cách quang tâm của thấu kính một khoảng d (cm) > 30 (cm) thì được ảnh thật A’B’ của thấu kính một khoảng d’ (cm) ( Hình 3.5). Ngược lại, nếu 0
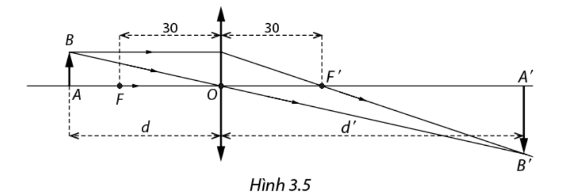
a, Từ công thức của thấu kính, hãy tìm biểu thức xác định hàm số d’= h (d)
b, Tìm các giới hạn \(\mathop {\lim }\limits_{x \to {{30}^ + }} h(d),\mathop {\lim }\limits_{x \to {{30}^ - }} h(d)\) và \(\mathop {\lim }\limits_{x \to + \infty } h(d)\). Sử dụng các kết quả này để giải thích ý nghĩa đã biết trong Vật lí.

a, Từ công thức rút d’ theo d.
b, Sử dụng giới hạn trái, giới hạn phải, giới hạn tại vô cực.
Advertisements (Quảng cáo)

a, Ta có : \(h(d) = \frac{1}{d} + \frac{1}{{d’}} = \frac{1}{{30}} \Rightarrow \frac{1}{{d’}} = \frac{1}{{30}} - \frac{1}{d} = \frac{{d - 30}}{{30d}} \Rightarrow d’ = \frac{{30d}}{{d - 30}}\)
b, Ta có: \(\mathop {\lim }\limits_{d \to {{30}^ + }} 30d = 900\), \(\mathop {\lim }\limits_{d \to {{30}^ + }} (d - 30) = 0\) và d-30 > 0
\( \Rightarrow \mathop {\lim }\limits_{d \to {{30}^ + }} h(d) = \mathop {\lim }\limits_{d \to {{30}^ + }} \frac{{30d}}{{d - 30}} = + \infty \)
Ta có: \(\mathop {\lim }\limits_{d \to {{30}^ - }} 30d = 900\), \(\mathop {\lim }\limits_{d \to {{30}^ - }} (d - 30) = 0\) và d – 30
\( \Rightarrow \mathop {\lim }\limits_{d \to {{30}^ - }} h(d) = \mathop {\lim }\limits_{d \to {{30}^ - }} \frac{{30d}}{{d - 30}} = - \infty \)
Ta có: \(\mathop {\lim }\limits_{d \to + \infty } h(d) = \mathop {\lim }\limits_{d \to + \infty } \frac{{30d}}{{d - 30}} = \mathop {\lim }\limits_{d \to + \infty } \frac{{30}}{{1 - \frac{{30}}{d}}} = 30\).
