I. Hàm số liên tục tại một điểm và liên tục trên một khoảng
1. Hàm số liên tục tại 1 điểm
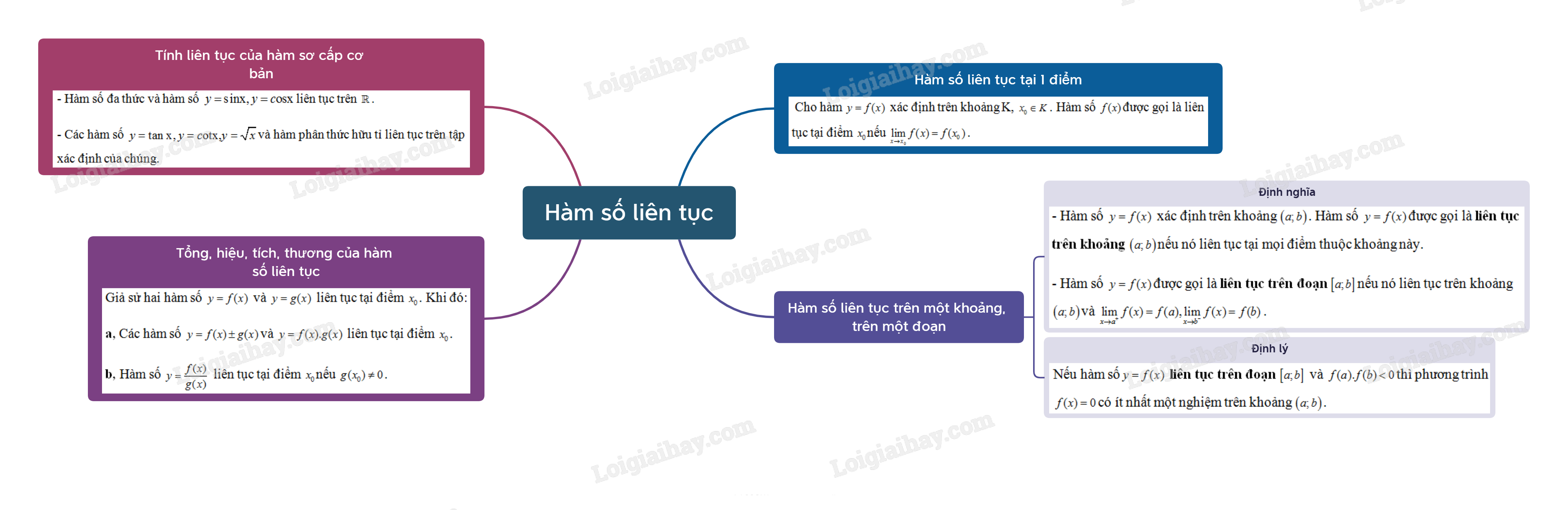
Cho hàm \(y = f(x)\) xác định trên khoảng K, \({x_0} \in K\). Hàm số \(f(x)\) được gọi là liên tục tại điểm \({x_0}\) nếu \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = f({x_0})\).
Hàm số không liên tục tại \({x_0}\) được gọi là gián đoạn tại điểm đó.
2. Hàm số liên tục trên một khoảng
- Hàm số \(y = f(x)\) xác định trên khoảng \(\left( {a;b} \right)\)
Hàm số \(y = f(x)\) được gọi là liên tục trên khoảng \(\left( {a;b} \right)\) nếu nó liên tục tại mọi điểm thuộc khoảng này.
- Hàm số \(y = f(x)\) được gọi là liên tục trên đoạn \(\left[ {a;b} \right]\) nếu nó liên tục trên khoảng \(\left( {a;b} \right)\) và \(\mathop {\lim }\limits_{x \to {a^ + }} f(x) = f(a),\mathop {\lim }\limits_{x \to {b^ - }} f(x) = f(b)\).
* Nhận xét:
- Đồ thị hàm số liên tục trên một khoảng, đoạn là “đường liền” trên khoảng, đoạn đó.
- Nếu hàm số\(y = f(x)\) liên tục trên đoạn \(\left[ {a;b} \right]\) và \(f(a).f(b)
Advertisements (Quảng cáo)
II. Một số định lý cơ bản
1. Định lý 1
- Hàm số đa thức và hàm số \(y = {\mathop{\rm s}\nolimits} {\rm{inx}},y = c{\rm{osx}}\)liên tục trên \(\mathbb{R}\).
- Các hàm số \(y = \tan {\rm{x}},y = c{\rm{otx,}}y = \sqrt x \) và hàm phân thức hữu tỉ (thương của hai đa thức) liên tục trên tập xác định của chúng.
2. Định lý 2
Giả sử hai hàm số \(y = f(x)\) và \(y = g(x)\) liên tục tại điểm \({x_0}\). Khi đó:
a, Các hàm số \(y = f(x) \pm g(x)\) và \(y = f(x).g(x)\) liên tục tại điểm \({x_0}\).
b, Hàm số \(y = \frac{{f(x)}}{{g(x)}}\) liên tục tại điểm \({x_0}\) nếu \(g({x_0}) \ne 0\).
c, Hàm số \(y = f(x)\) liên tục trên khoảng K và \(f(x) \ge 0,\forall x \in K\). Khi đó hàm số \(y = \sqrt {f(x)} \) liên tục trên K.