
Cho hình chóp S.ABCD có \(SA \bot (ABCD)\) và đáy là hình vuông. Gọi M là hình chiếu vuông góc của A trên SB. Chứng minh \(AM \bot (SBC)\) và \(BD \bot SC\).

Chứng minh \(BC \bot \left( {SAB} \right)\) từ đó suy ra \(BC \bot AM\)
Chứng minh \(AM \bot \left( {SBC} \right)\) dựa vào chứng minh \(AM \bot BC\) và \(SB\)
Chứng minh \(BD \bot \left( {SAC} \right)\) từ đó suy ra \(BD \bot SC\)

Advertisements (Quảng cáo)
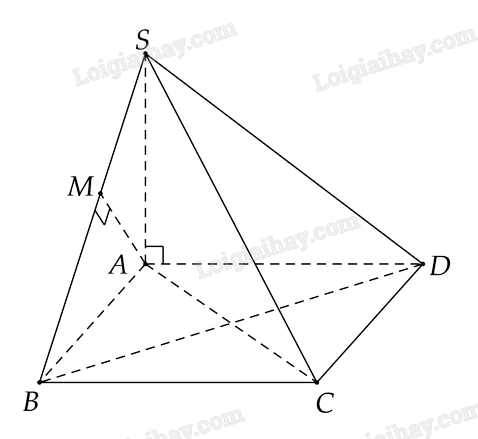
+) Vì \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot BC\)
Vì \(\left\{ \begin{array}{l}BC \bot SA\\BC \bot AB\,\,\left( {gt} \right)\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right)\). Mà \(AM \subset \left( {SAB} \right) \Rightarrow BC \bot AM\)
Vì \(\left\{ \begin{array}{l}AM \bot BC\\AM \bot SB\,\,\left( {gt} \right)\end{array} \right. \Rightarrow AM \bot \left( {SBC} \right)\)
+) Ta có \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot BD\)
Vì \(\left\{ \begin{array}{l}BD \bot SA\\BD \bot AC\,\,\left( {gt} \right)\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right) \Rightarrow BD \bot SC\)
