Hoạt động 1
Dòng 1 của bảng dưới đây cho biết biểu thức của một hàm số. Dòng 2 cho biết đồ thị của hàm số đã cho. Trả lời các câu hỏi ở dòng 3 và 4
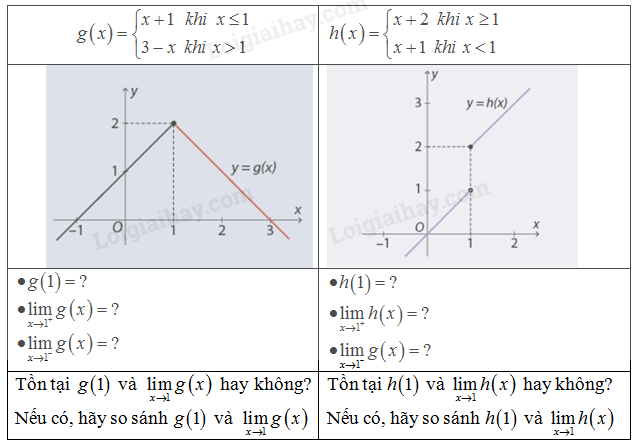

Với \(x = 1\) nên dựa vào điều kiện \(x \le 1\) để tính \(g\left( 1 \right)\) thì thay vào hàm số \(g\left( x \right) = x + 1\)
Với \(h\left( 1 \right)\) tính tương tự như \(g\left( 1 \right)\)
Khi \(x \to {1^ + }\) tức là \(x \ge 1\) nên phải tính\(\,\mathop {\lim }\limits_{x \to {1^ + }} g\left( x \right)\) ứng với hàm số \(g\left( x \right) = x + 1\)
Còn khi \(x \to {1^ - }\) tức là \(x
Hàm \(h\left( x \right)\) thì làm tương tự như hàm \(g\left( x \right)\)


Luyện tập 1
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{{x^2} - x - 6}}{{x + 2}}\,\,\,khi\,\,x \ne 2\\\,\,\,\,\,\,\,\,\,\,\,\,\,\, - 6\,\,\,khi\,\,x = - 2\end{array} \right.\). Xét tính liên tục của hàm số tại \({x_0} = - 2\)

Hàm số liên tục tại \({x_0} = - 2\) nếu \(\mathop {\lim }\limits_{x \to - 2} f\left( x \right) = f\left( { - 2} \right)\)
Đây là giới hạn tại điểm dạng vô định \(\frac{0}{0}\) nên phải thực hiện khử mẫu
Đây là hàm phân thức hữu tỉ nên ta thực hiện phân tích đa thức thành nhân tử để khử dạng vô định

Tập xác định của hàm số là \(\mathbb{R}\)
Advertisements (Quảng cáo)
Khi \(x = - 2\), ta có \(f\left( { - 2} \right) = - 6\)
\(\mathop {\lim }\limits_{x \to - 2} f\left( x \right) = \mathop {\lim }\limits_{x \to - 2} \frac{{{x^2} - x - 6}}{{x + 2}} = \mathop {\lim }\limits_{x \to - 2} \frac{{\left( {x + 2} \right)\left( {x - 3} \right)}}{{x + 2}} = \mathop {\lim }\limits_{x \to - 2} \left( {x - 3} \right) = - 2 - 3 = - 5\)
Vì \( - 5 \ne - 6\) \( \Rightarrow \) \(\mathop {\lim }\limits_{x \to - 2} f\left( x \right) \ne f\left( { - 2} \right)\) do đó hàm số không liên tục tại \({x_0} = - 2\)
Hoạt động 2
Xét tính liên tục của hàm số \(f\left( x \right) = {x^2} + 1\) tại điểm \({x_0}\) bất kì thuộc \(\mathbb{R}\)

Hàm số liên tục tại \(x = {x_0}\) nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)

Tập xác định của hàm số là \(\mathbb{R}\)
Khi \(x = {x_0}\) thì \(f\left( {{x_0}} \right) = x_0^2 + 1\)
\(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \left( {{x^2} + 1} \right) = x_0^2 + 1 = f\left( {{x_0}} \right)\)
Vậy hàm số \(f\left( x \right)\) liên tục tại điểm \({x_0}\) bất kì thuộc \(\mathbb{R}\)
Luyện tập 2
Xét tính liên tục của hàm số \(f\left( x \right) = \frac{{{x^2} - 1}}{{x - 1}}\) trên \(\left( {1; + \infty } \right)\)

Hàm số liên tục trên một khoảng nếu nó liên tục tại mọi điểm thuộc khoảng đó.

Hàm số có tập xác định là \(\left( { - \infty ;1} \right) \cup \left( {1; + \infty } \right)\)
Với mọi \({x_0} > 1\), ta có \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{{x^2} - 1}}{{x - 1}} = \frac{{x_0^2 - 1}}{{{x_0} - 1}} = f\left( {{x_0}} \right)\). Vậy hàm số liên tục tại mọi điểm \({x_0} > 1\) nên hàm số liên tục trên \(\left( {1; + \infty } \right)\)
