Hoạt động 1
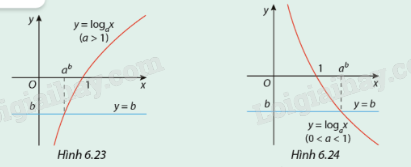
Quan sát các đồ thị ở trên và hãy biện luận theo b số giao điểm của đồ thị hàm số \(y = {\log _a}x\) và đường thẳng y = b.

Quan sát hình vẽ.

Xét phương trình hoành độ giao điểm \({\log _a}x = b\)
Phương trình luôn có nghiệm duy nhất \(x = {a^b}\forall b\)
Luyện tập 1
Giải các phương trình
a) \({\log _2}\left( {2x + 6} \right) + {\log _2}x = 3\)
Advertisements (Quảng cáo)
b) \(\log x = \log \left( {{x^2} + x - 1} \right)\)

\(b = {\log _a}A \Leftrightarrow {\log _a}A = {\log _a}B \Leftrightarrow \left\{ \begin{array}{l}A > 0\\B > 0\\A = B\end{array} \right.\)

a) Điều kiện: \(\left\{ \begin{array}{l}2x + 6 > 0\\x > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > - 3\\x > 0\end{array} \right. \Leftrightarrow x > 0\)
\(\begin{array}{l}{\log _2}\left( {2x + 6} \right) + {\log _2}x = 3\\ \Leftrightarrow {\log _2}\left[ {\left( {2x + 6} \right)x} \right] = {\log _2}8\\ \Leftrightarrow 2{x^2} + 6x = 8\\ \Leftrightarrow 2{x^2} + 6x - 8 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 1\left( {{\rm{TM}}} \right)\\x = - 4\left( {\rm{L}} \right)\end{array} \right.\end{array}\)
Vậy phương trình có nghiệm là x = 1
b) Điều kiện: x > 0
\(\begin{array}{l}\log x = \log \left( {{x^2} + x - 1} \right)\\ \Leftrightarrow x = {x^2} + x - 1\\ \Leftrightarrow {x^2} - 1 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 1\left( {{\rm{TM}}} \right)\\x = - 1\left( {\rm{L}} \right)\end{array} \right.\end{array}\)
Vậy phương trình có tập nghiệm là x = 1
