Hoạt động 2
Ta biết: Với (C1) là đồ thị của hàm số y = f(x) và (C2) là đồ thị của hàm số y = g(x) thì tập hợp giá trị của x để (C1) nằm phía trên (C2) là tập nghiệm của bất phương trình f(x) > g(x).
Quan sát các đồ thị (Hình 6.23 và 6.24) trong Hoạt động 1 và trong mỗi trường hợp, hãy tìm các tập nghiệm của bất phương trình \({\log _a}x > b\).
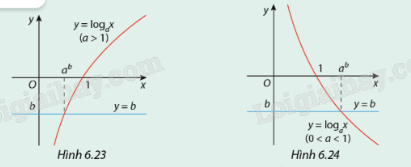

Quan sát hình vẽ.

Nếu a > 1: \({\log _a}x > b \Leftrightarrow x > {a^b}\)
Nếu 0 b \Leftrightarrow 0
Luyện tập 2
Giải các bất phương trình:
a) \({\log _{0,2}}\left( {2x - 3} \right) \le 1\)
Advertisements (Quảng cáo)
b) \(\ln \left( {2x + 3} \right) \le \ln \left( {3x + 1} \right)\)

Đưa \({\log _a}A > \alpha \) về dạng \({\log _a}A > {\log _a}B\)
Nếu a > 1: \({\log _a}A > {\log _a}B \Leftrightarrow A > B > 0\)
Nếu 0 {\log _a}B \Leftrightarrow 0

a)
\(\begin{array}{l}{\log _{0,2}}\left( {2x - 3} \right) \le 1\\ \Leftrightarrow {\log _{0,2}}\left( {2x - 3} \right) \le {\log _{0,2}}0,2\\ \Leftrightarrow 2x - 3 > 0,2\\ \Leftrightarrow x > 1,6\end{array}\)
Vậy bất phương trình có tập nghiệm là \(\left[ {\left. {1,6; + \infty } \right)} \right.\)
b)
\(\begin{array}{l}\ln \left( {2x + 3} \right) \le \ln \left( {3x + 1} \right)\\ \Leftrightarrow 0 - \frac{3}{2}\\x \ge 2\end{array} \right. \Leftrightarrow x \ge 2\end{array}\)
Vậy bất phương trình có tập nghiệm là \(\left[ {\left. {2; + \infty } \right)} \right.\)
