Hoạt động 1
Một vật bắt đầu chuyển động theo đường thẳng và quãng đường đi được sau t giây được tính bởi \(s(t) = 2{t^2}\), s(t) tính bằng mét.
a, Cho biết vận tốc trung bình ( đơn vị m/s) của vật trong khoảng thời gian [\({t_0};t\)] được tính bởi công thức \({v_{tb}} = \frac{{s(t) - s({t_0})}}{{t - {t_0}}}\). Hãy tính vận tốc trung bình trong các khoảng thời gian [\({t_0};t\)] với \({t_0} = 3\)và t lần lượt là 3,1 ; 3,01 ; 3,001. Sau đó hoàn thành Bảng 7.1
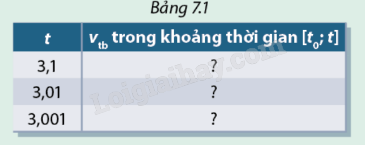
b, Vận tốc trung bình trong khoảng thời gian nào ở Bảng 7.1 gần nhất với vận tốc tại thời điểm \({t_0} = 3\)
c, Để vận tốc trung bình trong khoảng thời gian [\({t_0};t\)] càng gần với vận tốc tại thời điểm \({t_0}\)thì ta cần chọn giá trị của t như thế nào?

a, Áp dụng công thức \(s(t) = 2{t^2}\) và công thức \({v_{tb}} = \frac{{s(t) - s({t_0})}}{{t - {t_0}}}\) để tính vận tốc trung bình.
b, Dựa vào kết quả câu a để tìm giá trị vận tốc gần với vận tốc tại thời điểm \({t_0} = 3\)
c, Để vận tốc trung bình càng gần vận tốc tại thời điểm \({t_0}\)thì ta cần chọn giá trị của t càng gần thời điểm \({t_0}\).

a, Thay t = 3,1; t=3,01; t= 3,001 vào hàm số s(t) ta được:
\(s(3,1) = 2.3,{1^2} = 2.9,61 = 19,22\)\( \Rightarrow {v_{tb}} = \frac{{s(3,1) - s(3)}}{{3,1 - 3}} = \frac{{19,22 - 18}}{{0,1}} = 12,2\)
\(s(3,01) = 2.3,{01^2} = 2.9,0601 = 18,1202\)\( \Rightarrow {v_{tb}} = \frac{{s(3,01) - s(3)}}{{3,01 - 3}} = \frac{{18,1202 - 18}}{{0,01}} = 12,02\)
\(s(3,001) = 2.3,{001^2} = 2.9,006001 = 18,012002\)\( \Rightarrow {v_{tb}} = \frac{{s(3,001) - s(3)}}{{3,001 - 3}} = \frac{{18,012002 - 18}}{{0,001}} = 12,002\)

b, Từ kết quả câu a cho thấy vận tốc tại thời điểm t = 3,001 gần nhất với vận tốc tại thời điểm \({t_0} = 3\)
c, Từ kết quả câu b ta thấy để vận tốc trung bình càng gần vận tốc tại thời điểm \({t_0}\)thì ta cần chọn giá trị của t càng gần thời điểm \({t_0}\).
Luyện tập 1
Advertisements (Quảng cáo)
Tính đạo hàm của hàm số \(f(x) = \frac{2}{{x + 1}}\) tại điểm \({x_0} = 1\)

Sử dụng định nghĩa đạo hàm của hàm số tại một điểm

Ta có: \(\mathop {\lim }\limits_{x \to 1} \frac{{f(x) - f(1)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\frac{2}{{x + 1}} - 1}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{1 - x}}{{(x + 1).(x - 1)}}\mathop { = \lim }\limits_{x \to 1} \frac{{ - 1}}{{x + 1}} = \frac{{ - 1}}{2}\)
Vận dụng
Xét tình huống vận động viên nhảy dù trong bài toán khởi động:
a, Tìm vận tốc của vận động viên nhảy dù sau 2 giây kể từ khi bắt đầu rơi tự do
b, Sau khi rơi tự do được 490 m, vận động viên đó bung dù để chuẩn bị đáp xuống mặt đất. Tìm vận tốc của vận động viên tại thời điểm bung dù.

a, Vận tốc của vận động viên sau 2 giây kể từ khi rơi tự do là đạo hàm của hàm số tại \({t_0} = 2\).
b, Tìm thời điểm mà vận động viên đi được 490 m, sau đó tính đạo hàm của hàm số tại thời điểm đó để xác định vận tốc tức thời.

a, Vận tốc của vận động viên sau 2 giây kể từ khi rơi tự do là:
\(\mathop {\lim }\limits_{t \to 2} \frac{{f(t) - f(2)}}{{t - 2}} = \mathop {\lim }\limits_{t \to 2} \frac{{4,9{t^2} - 19,6}}{{t - 2}} = \mathop {\lim }\limits_{t \to 2} \frac{{4,9.({t^2} - 4)}}{{t - 2}} = \mathop {\lim }\limits_{t \to 2} \frac{{4,9.(t - 2).(t + 2)}}{{t - 2}} = \mathop {\lim }\limits_{t \to 2} 4,9.(t + 2) = 19,6\)
Vậy vận tốc của vận động viên sau 2 giây kể từ khi rơi tự do là 19,6 m / s
b, Ta có: \(s({t_1}) = 4,9{t_1}^2 \Leftrightarrow 490 = 4,9.{t_1}^2 \Leftrightarrow {t_1}^2 = 100 \Rightarrow {t_1} = 10\)
Vận tốc của vận động viên tại thời điểm bung dù là:
\(\mathop {\lim }\limits_{t \to 10} \frac{{f(t) - f(10)}}{{t - 10}} = \mathop {\lim }\limits_{t \to 2} \frac{{4,9{t^2} - 490}}{{t - 10}} = \mathop {\lim }\limits_{t \to 2} \frac{{4,9.({t^2} - 100)}}{{t - 10}} = \mathop {\lim }\limits_{t \to 2} \frac{{4,9.(t - 10).(t + 10)}}{{t - 10}} = \mathop {\lim }\limits_{t \to 10} 4,9.(t + 10) = 98\)
Vậy vận tốc của vận động viên tại thời điểm bung dù là 98 m/s
