Hoạt động 3
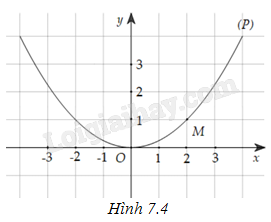
Cho hàm số \(f(x) = \frac{{{x^2}}}{4}\) có đồ thị là đường parabol (P) như Hình 7.4 . Gọi M là điểm thuộc (P) có hoành độ \({x_0} = 2\).
a, Tính \({f’}(2)\)
b, Viết phương trình đường thẳng \(\Delta \) đi qua điểm M và có hệ số góc bằng \({f’}(2)\)
c, Vẽ đường thẳng \(\Delta \) và (P) trên cùng một mặt phẳng tọa độ. Có nhận xét gì về \(\Delta \) và (P).

a, Áp dụng định nghĩa tính \({f’}(2)\)
b, Phương trình đường thẳng đi qua điểm M có hoành độ \({x_0}\) và hệ số góc \({f’}(2)\) là
\(y = {f’}({x_0}).(x - {x_0})\)
c, Dựa vào câu b để vẽ đường thẳng \(\Delta \)

a, Ta có: \({f’}(2) = \mathop {\lim }\limits_{x \to 2} \frac{{f(x) - f(2)}}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} \frac{{\frac{{{x^2}}}{4} - 1}}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} \frac{{{x^2} - 4}}{{4(x - 2)}} = \mathop {\lim }\limits_{x \to 2} \frac{{(x - 2).(x + 2)}}{{4(x - 2)}} = \mathop {\lim }\limits_{x \to 2} \frac{{x + 2}}{4} = 1\)
b, Điểm M có tọa độ M(2;1)
Phương trình đường thẳng \(\Delta \) đi qua điểm M(2,1) có hệ số góc \({f’}(2)\) là:
y = 1.( x-2)+1= x-1
Vậy phương trình đường thẳng \(\Delta \) là: y= x-1
Luyện tập 2
Cho hàm số \(y = - 3{x^3}\) có đồ thị ( C ). Tìm hệ số góc của tiếp tuyến tại điểm M (-1,3)

Hệ số góc của tiếp tuyến là đạo hàm của hàm số tại điểm -1

Ta có: \({f’}( - 1) = \mathop {\lim }\limits_{x \to - 1} \frac{{f(x) - f( - 1)}}{{x - ( - 1)}} = \mathop {\lim }\limits_{x \to - 1} \frac{{ - 3{x^3} - 3}}{{x + 1}} = \mathop {\lim }\limits_{x \to - 1} \frac{{ - 3.({x^3} + 1)}}{{x + 1}} = \mathop {\lim }\limits_{x \to - 1} ( - 3).({x^2} - x + 1) = - 9\)
Advertisements (Quảng cáo)
Vậy hệ số góc của tiếp tuyến tại điểm M(-1,3) là -9.
Hoạt động 4
Cho hàm số \(f(x) = {x^2} + 1\)có đồ thị parabol (P) và điểm M(1,2) thuộc (P). Gọi \(\Delta \)là tiếp tuyến của (P) tại M. Hãy viết phương trình \(\Delta \).

Hệ số góc của tiếp tuyến là đạo hàm của hàm số tại điểm 1
Phương trình tiếp tuyến của đường thẳng có hệ số góc k tại điểm \(M({x_0};{y_0})\) là:
\(y = k.(x - {x_0}) + {y_0}\)

Ta có: \(y'(1) = \mathop {\lim }\limits_{x \to 1} \frac{{f(x) - f(1)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{{x^2} + 1 - 2}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} (x + 1) = 2\)
Phương trình tiếp tuyến tại điểm M(1,2) có hệ số góc k=2 là:
y = 2.( x -1)+2=2x
Luyện tập 3
Cho parabol (P) \(y = {x^2} + 2x - 3\) và điểm M thuộc (P) có hoành độ \({x_0} = - 2\)
a, Tính \({y’}( - 2)\)
b, Viết phương trình tiếp tuyến của (P) tại điểm M.

a, Sử dụng định nghĩa để tìm đạo hàm của hàm số tại điểm -2
b, Sử dụng công thức tiếp tuyến \(y = {f’}({x_0}).(x - {x_0}) + f({x_0})\)

a, Ta có: \(y'( - 2) = \mathop {\lim }\limits_{x \to - 2} \frac{{f(x) - f( - 2)}}{{x + 2}} = \mathop {\lim }\limits_{x \to - 2} \frac{{{x^2} + 2x - 3 - ( - 3)}}{{x + 2}} = \mathop {\lim }\limits_{x \to - 2} \frac{{{x^2} + 2x}}{{x + 2}} = \mathop {\lim }\limits_{x \to - 2} \frac{{x.(x + 2)}}{{x + 2}} = \mathop {\lim }\limits_{x \to - 2} x = - 2\)
b, Ta có: \({x_0} = - 2 \Rightarrow f({x_0}) = {( - 2)^2} + 2.( - 2) - 3 = - 3\)
Phương trình tiếp tuyến của (P) tại điểm M (-2, -3) là:
y = -2. (x + 2) -3= -2x -7.
