Hoạt động 3
Các hàm số \(f\left( x \right) = {x^3} - 3x + 2\) và \(g\left( x \right) = \sin x\) xác định trên \(\left( { - \infty ; + \infty } \right)\) có đồ thị như sau:
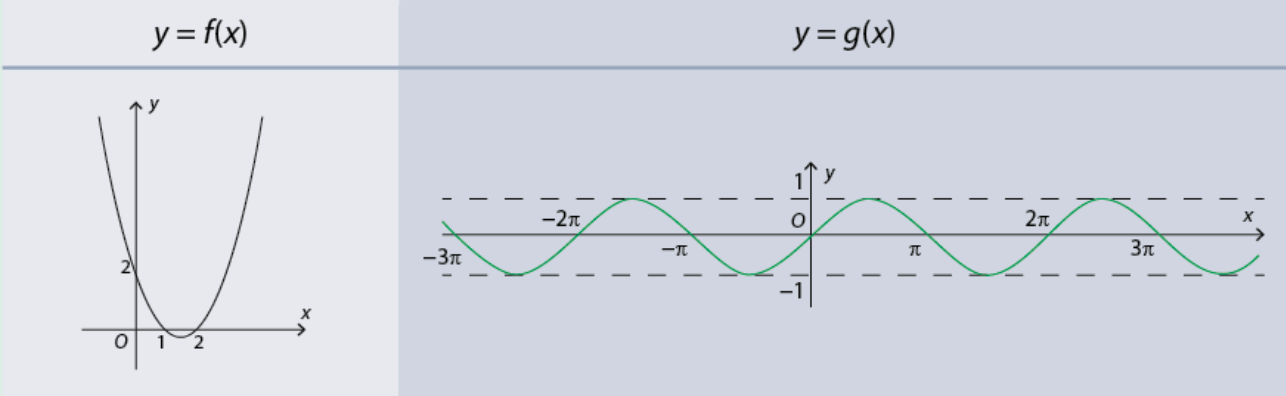
Dựa vào đồ thị, hãy dự đoán tính liên tục của các hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) trên \(\left( { - \infty ; + \infty } \right)\).

Đồ thị hàm số liên tục trên một khoảng là đường liền trên khoảng đó

Quan sát đồ thị hàm số \(y = f\left( x \right),y = g\left( x \right)\) ta thấy chúng là một đường nét liền trên \(\left( { - \infty ; + \infty } \right)\) nên hai hàm số đó liên tục trên \(\left( { - \infty ; + \infty } \right)\)
Luyện tập 3
Xét tính liên tục của hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{{x^3} + x - 2}}{{x - 1}}\,\,\,khi\,\,x \ne 1\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2\,\,\,khi\,\,x = 1\end{array} \right.\) trên \(\mathbb{R}\)

Hàm số liên tục trên \(\mathbb{R}\) nếu nó liên tục tại mọi điểm thuộc \(\mathbb{R}\)
Hàm số phân thức hữu tỉ (thương của hai đa thức) liên tục trên từng khoảng xác định của chúng.
Xét tính liên tục của hàm số \(f\left( x \right)\) tại điểm \(x = 1\)

Tập xác định của hàm số là \(\mathbb{R}\)
+ Trên tập \(\left( { - \infty ;1} \right) \cup \left( {1; + \infty } \right)\), hàm số \(f\left( x \right) = \frac{{{x^3} + x - 2}}{{x - 1}}\) là phân thức hữu tỉ xác định trên các khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\) nên liên tục trên các khoảng này.
+ Khi \(x = 1\), ta có \(f\left( 1 \right) = 2\).
\(\mathop {\lim }\limits_{x \to 1} f\left( x \right) = \mathop {\lim }\limits_{x \to 1} \frac{{{x^3} + x - 2}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\left( {x - 1} \right)\left( {{x^2} + x + 2} \right)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \left( {{x^2} + x + 2} \right) = {1^2} + 1 + 2 = 4 \ne f\left( 1 \right)\)
Vậy hàm số \(f\left( x \right)\) không liên tục tại \(x = 1\)
Suy ra hàm số đã cho gián đoạn tại \(x = 1\) hay hàm số \(f\left( x \right)\) không liên tục trên \(\mathbb{R}\)
Hoạt động 4
Cho hàm số \(f\left( x \right) = {x^2}\) và \(g\left( x \right) = \frac{1}{x}\).
a) Xét tính liên tục của \(y = f\left( x \right)\) và \(y = g\left( x \right)\) tại \({x_0} = 1\).
b) Xét tính liên tục của hàm số \(y = f\left( x \right) + g\left( x \right)\) tại \({x_0} = 1\).

Hàm số liên tại tại điểm \(x = {x_0}\) nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)
Tính \(f\left( {{x_0}} \right)\) và \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right)\) rồi so sánh chúng
Tương tự với hàm \(y = g\left( x \right)\) và \(y = f\left( x \right) + g\left( x \right)\)

a)
+ Hàm số \(y = f\left( x \right) = {x^2}\) có TXĐ là \(\mathbb{R}\)
Với \({x_0} = 1 \Rightarrow f\left( 1 \right) = {1^2} = 1\)
\(\mathop {\lim }\limits_{x \to 1} f\left( x \right) = \mathop {\lim }\limits_{x \to 1} {x^2} = {1^2} = 1 = f\left( 1 \right)\). Suy ra, hàm số \(y = f\left( x \right)\) liên tục tại \({x_0} = 1\)
+ Hàm số \(y = g\left( x \right) = \frac{1}{x}\) có tập xác định là \(\mathbb{R}\backslash \left\{ 0 \right\}\)
Với \({x_0} = 1 \Rightarrow g\left( 1 \right) = \frac{1}{1} = 1\)
Advertisements (Quảng cáo)
\(\mathop {\lim }\limits_{x \to 1} g\left( x \right) = \mathop {\lim }\limits_{x \to 1} \frac{1}{x} = \frac{1}{1} = 1 = f\left( 1 \right)\). Suy ra, hàm số \(y = f\left( x \right)\) liên tục tại \({x_0} = 1\)
b) Với \({x_0} = 1 \Rightarrow f\left( 1 \right) + g\left( 1 \right) = {1^2} + \frac{1}{1} = 2\)
\(\mathop {\lim }\limits_{x \to 1} \left( {f\left( x \right) + g\left( x \right)} \right) = \mathop {\lim }\limits_{x \to 1} \left( {{x^2} + \frac{1}{x}} \right) = {1^2} + \frac{1}{1} = 2 = f\left( 1 \right) + g\left( 1 \right)\).
Suy ra, hàm số \(y = f\left( x \right) + g\left( x \right)\) liên tục tại \({x_0} = 1\)
Luyện tập 4
Tìm các khoảng trên đó hàm số sau đây là liên tục: \(y = x + \tan x\)

Hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) là các hàm số liên tục trên khoảng K thì hàm số \(y = f\left( x \right) \pm g\left( x \right)\) cũng liên tục trên khoảng K
Hàm số \(y = \tan x,y = \cot x\) liên tục trên từng khoảng xác định của chúng
Tìm tập xác định của hàm số

Xét hàm số \(f\left( x \right) = x\) và \(g\left( x \right) = \tan x\)
+ Hàm số \(f\left( x \right) = x\) là hàm đa thức nên \(f\left( x \right)\) liên tục trên \(\mathbb{R}\)
+ Hàm số \(g\left( x \right) = \tan x\) có tập xác định là \(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}\) nên hàm số \(g\left( x \right)\) liên tục trên các khoảng \(\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}} \right)\)
Do đó, hàm số \(y = f\left( x \right) + g\left( x \right) = x + \tan x\) liên tục trên các khoảng \(\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}} \right)\)
Vận dụng
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}x + 1\,\,khi\,\,x \le 0\\ax + b\,\,khi\,\,0

Hàm số liên tục trên \(\mathbb{R}\) nếu nó liên tục tại mọi điểm thuộc \(\mathbb{R}\)
Dựa tính liên tục tại các điểm \(x = 0;x = 2\) để tìm \(a\) và \(b\)

Tập xác định của hàm số là \(\mathbb{R}\)
Với \(x
Với \(0
Với \(x > 2\), hàm số \(f\left( x \right) = 4 - x\) là hàm đa thức nên hàm số liên tục trên khoảng \(\left( {2; + \infty } \right)\)
Để hàm số liên tục trên \(\mathbb{R}\) thì hàm số \(y = f\left( x \right)\) phải liên tục tại các điểm \(x = 0\) và \(x = 2\)
+ Với \(x = 0 \Rightarrow f\left( 0 \right) = 0 + 1 = 1\)
\(\mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} \left( {x + 1} \right) = 0 + 1 = 1\)
\(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} \left( {ax + b} \right) = a.0 + b = b\)
Để hàm số liên tục tại \(x = 0\) thì \(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = f\left( 0 \right) \Leftrightarrow b = 1\) \(\left( 1 \right)\)
+ Với \(x = 2 \Rightarrow f\left( 2 \right) = 4 - 2 = 2\)
\(\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} \left( {ax + b} \right) = 2a + b\)
\(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} \left( {4 - x} \right) = 4 - 2 = 2\)
Để hàm số liên tục tại \(x = 2\) thì \(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = f\left( 2 \right) \Leftrightarrow 2a + b = 2\) \(\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\), suy ra \(\left\{ \begin{array}{l}b = 1\\2a + b = 2\end{array} \right. \Leftrightarrow a = \frac{1}{2};b = 1\)
