
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và \(\widehat {BAD} = {60^0}\). Biết \(SA \bot (ABCD)\) và \(SA = a\).
a) Chứng minh rằng \(BD \bot SC\).
b) Tính theo a khoảng cách giữa hai đường thẳng BD và SC.

Nếu đường vuông góc chung \(\Delta \) cắt a, b tương ứng tại M, N thì độ dài đoạn thẳng MN được gọi là khoảng cách giữa hai đường thẳng chéo nhau a, b.

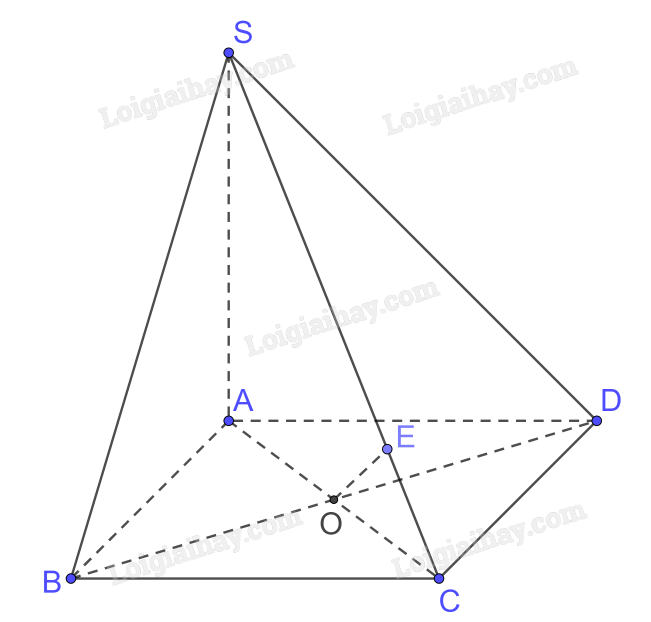
a) Ta có \(BD \bot AC,BD \bot SA \Rightarrow BD \bot \left( {SAC} \right);SC \subset \left( {SAC} \right) \Rightarrow BD \bot SC\)
b) Trong (SAC) kẻ \(OE \bot SC\)
Advertisements (Quảng cáo)
Mà \(BD \bot \left( {SAC} \right) \Rightarrow OE \bot BD\)
\( \Rightarrow d\left( {BD,SC} \right) = OE\)
Gọi \(AC \cap BD = \left\{ O \right\}\)
Xét tam giác BAD có AB = AD, \(\widehat {BAD} = {60^0}\) \( \Rightarrow \) Tam giác BAD đều
\( \Rightarrow AO = \frac{{a\sqrt 3 }}{2} \Rightarrow AC = a\sqrt 3 \)
Xét tam giác SAC vuông tại A có
\(SC = \sqrt {S{A^2} + A{C^2}} = \sqrt {{a^2} + {{\left( {a\sqrt 3 } \right)}^2}} = 2a\)
Dễ dàng chứng minh được
\( \Rightarrow \frac{a}{{OE}} = \frac{{2a}}{{\frac{{a\sqrt 3 }}{2}}} \Rightarrow OE = \frac{{a\sqrt 3 }}{4}\)
Vậy \(d\left( {BD,SC} \right) = \frac{{a\sqrt 3 }}{4}\)
