Bài 2 trang 77 sách giáo khoa hình học lớp 11: Ôn tập Chương II - Đường thẳng và mặt phẳng trong không gian. Quan hệ song song. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P theo thứ tự à trung điểm của các đoạn thẳngSA, BC, CD. Tìm thiết diện của hình chóp khi cắt bởi mặt phẳng (MNP)
Bài 2. Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(M, N, P\) theo thứ tự là trung điểm của các đoạn thẳng \(SA, BC, CD\). Tìm thiết diện của hình chóp khi cắt bởi mặt phẳng \((MNP)\)
Gọi \(O\) là giao diểm hai đường chéo của hình bình hành \(ABCD\), hãy tìm giao điểm của đường thẳng \(SO\) với \(mp (MNP)\).
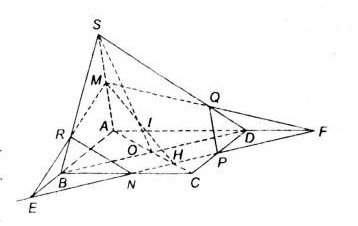
a) Trong mặt phẳng \((ABCD)\) đường thẳng \(NP\) cắt đường thẳng \(AB, AD\) lần lượt tại \(E, F\).
Trong mặt phẳng\((SAD)\) gọi \(Q=SD\cap MF\)
Advertisements (Quảng cáo)
Trong mặt phẳng\((SAB)\) gọi \(R=SB\cap ME\)
Từ đó ta có thiết dện là \(MQPNR\).
b) Trong \((ABCD)\) gọi \(H=AC\cap NP\)
Trong \((SAC)\): gọi \(I=SO ∩ MH\)
Vậy \(I=SO\cap(MNP)\)