77. Trang 65 Sách bài tập Hình học 11 nâng cao.
Cho hình hộp \(ABCD.{A_1}{B_1}{C_1}{D_1}.\)
a) Chứng minh rằng đường chéo \({B_1}D\) cắt \(mp\left( {{A_1}B{C_1}} \right)\) tại điểm G sao cho \({B_1}G = {1 \over 2}GD\) và G là trọng tâm của tam giác \({A_1}B{C_1}.\)
b) Chứng minh rằng \(\left( {{D_1}AC} \right)//\left( {B{A_1}{C_1}} \right)\) và trọng tâm G’ của tam giác \({D_1}AC\) cũng nằm trên \({B_1}D\) và \({B_1}G’ = {2 \over 3}{B_1}D.\)
c) Gọi P, Q, R lần lượt là các điểm đối xứng của điểm \({B_1}\) qua \(A,\,{D_1}\) và C. Chứng minh rằng \(\left( {PQR} \right)//\left( {B{A_1}{C_1}} \right)\).
d) Chứng minh rằng D là trọng tâm tứ diện \({B_1}PQR.\)

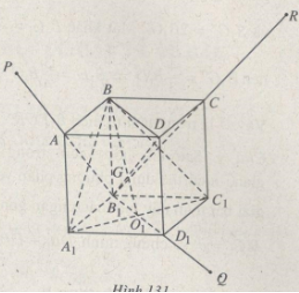
a) Gọi \({O_1}\) là giao điểm của \({A_1}{C_1}\) và \({B_1}{D_1}.\) Khi đó \(\left( {{A_1}B{C_1}} \right) \cap \left( {B{\rm{D}}{D_1}{B_1}} \right) = B{O_1}.\)
Gọi G là giao điểm của \({B_1}D\) và \(B{O_1}\) thì G chính là giao điểm của \({B_1}D\) với \(\left( {{A_1}B{C_1}} \right).\) Dễ thấy \(\Delta GBD \sim \Delta G{O_1}{B_1},\) tỉ số đồng dạng là 2 (do \({{BD} \over {{B_1}{O_1}}} = 2\)).
Vậy \({B_1}G = {1 \over 2}GD\) và \(G{O_1} = {1 \over 2}GB,\) suy ra G là trọng tâm tam giác \({A_1}B{C_1}.\)
Advertisements (Quảng cáo)
b) Dễ thấy
\(AC//{A_1}{C_1},\,{D_1}A//{C_1}B \Rightarrow \left( {{D_1}AC} \right)//\left( {B{A_1}{C_1}} \right).\)
Chứng minh tương tự như câu a), ta có trọng tâm G’ của tam giác \({D_1}AC\) nằm trên đường chéo \(D{B_1}\) và \(DG’ = {1 \over 2}G'{B_1}.\) Từ đó và kết quả của câu a), suy ra G và G’ chia đường chéo \({B_1}D\) thành ba phần bằng nhau.
Vậy \({B_1}G’ = {2 \over 3}{B_1}D.\)
c) Do \(A,\,{D_1},\,C\) lần lượt là trung điểm của \(P{B_1},\,Q{B_1},\,R{B_1}\) nên
\(PQ//A{D_1},\,QR//{D_1}C,\,RP//CA.\)
Từ đó suy ra: \(\left( {PRQ} \right)//\left( {A{D_1}C} \right).\)
Mặt khác, theo câu b), ta có \(\left( {{D_1}AC} \right)//\left( {B{A_1}{C_1}} \right),\) nên \(\left( {PRQ} \right)//\left( {B{A_1}{C_1}} \right).\)
d) Vì \(A,\,{D_1},\,C\) lần lượt là trung điểm của \({B_1}P,\,{B_1}Q,\,{B_1}R\) nên trọng tâm G” của tam giác PRQ phải nằm trên đường thẳng \({B_1}G’\) và \({B_1}G” = 2{B_1}G’.\) Mặt khác \({B_1}G’ = {2 \over 3}{B_1}D,\) nên
\({B_1}G” = {4 \over 3}{B_1}D \Rightarrow {B_1}D = {3 \over 4}{B_1}G”.\)
Vậy D là trọng tâm tứ diện \({B_1}PQR.\)
