Bài 4. Cho hình bình hành \(ABCD\). Qua \(A, B, C, D\) lần lượt vẽ bốn nửa đường thẳng \(Ax, By, Cz, Dt\) ở cùng phía đối với mặt phẳng \((ABCD)\), song song với nhau và không nằm trong mặt phẳng \((ABCD)\). Một mặt phẳng \((β)\) lần lượt cắt \(Ax, By, Cz\) và \(Dt\) tại \(A’, B’, C’\) và \(D’\).
a) Chứng minh mặt phẳng \((Ax, By)\) song song với mặt phẳng \(( Cz, Dt)\)
b) Gọi \(I = AC ∩ BD, J = A’C’ ∩ B’D’\). Chứng minh \(IJ\) song song với \(AA’\)
c) Cho \(AA’ = a, BB’ = b, CC’ = c\). Hãy tính \(DD’\).

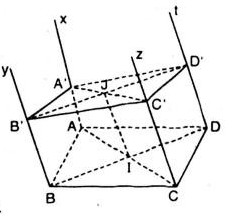
a) \(Ax // Dt\) (giả thiết) và \(AB // CD\) (vì \(ABCD\) là hình bình hành).
Do đó \((Ax, By) // ( Cz, Dt)\)
b) Ta có \((Ax, By) // ( Cz, Dt)\). Mặt phẳng \((A’B’C’D’)\) lần lượt cắt hai mặt phẳng \((Ax, By)\) và \(( Cz, Dt)\) theo giao tuyến \(A’B’\) và \(C’D’\) do đó \(A’B’//C’D’\).
Advertisements (Quảng cáo)
Tương tự ta chứng minh được: \(A’D’//B’C’\)
Do đó \(A’B’C’D’\) là hình bình hành.
\(J=A’C’\cap B’D’\) nên \(J\) là trung điểm của \(A’C’\)
Suy ra \(IJ\) là đường trung bình hình thang \(A’C’CA\) do đó \(Ị\) song song với \(AA’\).
c) Theo tính chất của đường trung bình hình thang ta có:
\(AA’+CC’=2IJ\)
\(BB’+DD’=2IJ\)
Do đó : \(DD’=AA’+CC’-BB’\)
\(DD’ = a + c - b\).
