Câu hỏi/bài tập:

Một cửa sổ gồm phần dưới là một hình chữ nhật và phần vòm có hình bán nguyệt được mô tả ở Hình 34. Tìm \(x,y\) để diện tích của cửa sổ lớn nhất, biết chu vi của cửa sổ là 5 m.
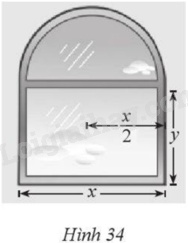

‒ Tìm công thức xác định hàm số mô phỏng diện tích của cửa sổ.
‒ Dựa vào công thức của hàm số để tìm giá trị lớn nhất của hàm số.

Chu vi của cửa sổ là: \(x + 2y + \frac{1}{2}.2\pi .\frac{x}{2} = x + 2y + \frac{{\pi x}}{2} = 5 \Leftrightarrow y = \frac{{10 - \left( {2 + \pi } \right)x}}{4}\).
Advertisements (Quảng cáo)
Vì chu vi của cửa sổ bằng 5 nên \(\frac{{10 - \left( {2 + \pi } \right)x}}{4} < 5 \Leftrightarrow \).
Diện tích của cửa sổ là: \(S = xy + \frac{1}{2}.\pi .{\left( {\frac{x}{2}} \right)^2} = x.\frac{{10 - \left( {2 + \pi } \right)x}}{4} + \frac{{\pi {x^2}}}{8} = \frac{{ - \left( {\pi + 4} \right){x^2} + 20{\rm{x}}}}{8}\)
Xét hàm số \(S\left( x \right) = \frac{{ - \left( {\pi + 4} \right){x^2} + 20{\rm{x}}}}{8}\) trên \(\left( {0; + \infty } \right)\).
Ta có: \(S’\left( x \right) = - \frac{{\pi + 4}}{4}x + \frac{5}{2}\)
Khi đó, trên khoảng \(\left( {0; + \infty } \right)\), \(S’\left( x \right) = 0\) khi \(x = \frac{{10}}{{\pi + 4}}\).
Bảng biến thiên:
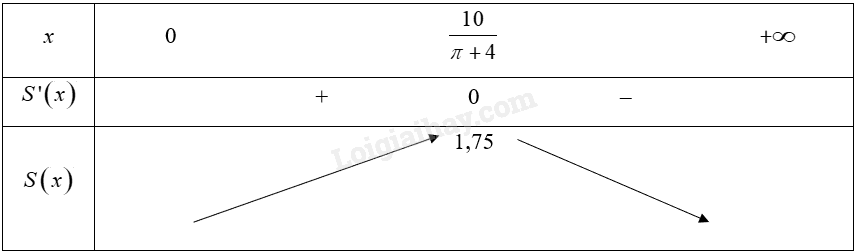
Vậy \(\mathop {\max }\limits_{\left( {0; + \infty } \right)} S\left( x \right) = 1,75\) tại \(x = \frac{{10}}{{\pi + 4}} \Leftrightarrow y = \frac{5}{{\pi + 4}}\).
Vậy khi \(x = \frac{{10}}{{\pi + 4}} \approx 1,4\left( m \right),y = \frac{5}{{\pi + 4}} \approx 0,7\left( m \right)\) thì diện tích của cửa sổ lớn nhất.
