Câu hỏi/bài tập:

Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\backslash \left\{ { - 2} \right\}\), liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
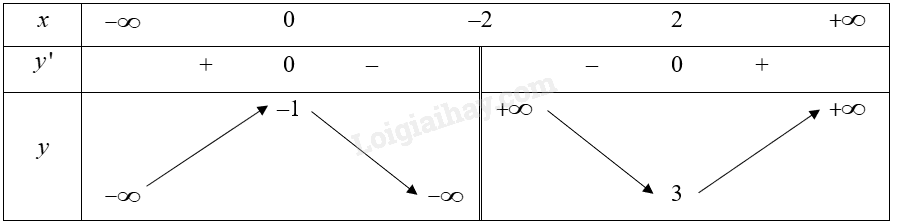
Khẳng định nào sau đây là đúng?
A. Đồ thị hàm số có tiệm cận đứng là đường thẳng \(x = - 2\) và không có tiệm cận ngang.
B. Đồ thị hàm số có tiệm cận đứng là đường thẳng \(x = - 2\) và tiệm cận ngang là đường thẳng \(y = 3\).
C. Đồ thị hàm số không có tiệm cận đứng và tiệm cận ngang là đường thẳng \(y = - 2\).
D. Đồ thị hàm số có tiệm cận đứng là đường thẳng \(x = - 2\) và tiệm cận ngang là đường thẳng \(y = 3\).

Advertisements (Quảng cáo)
‒ Tìm tiệm cận đứng: Tính \(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right)\) hoặc \(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right)\), nếu một trong các giới hạn sau thoả mãn: \(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = + \infty ;\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = - \infty ;\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = + \infty ;\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = - \infty \)
thì đường thẳng \(x = {x_0}\) là đường tiệm cận đứng.
‒ Tìm tiệm cận ngang: Nếu \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = {y_0}\) thì đường thẳng \(y = {y_0}\) là đường tiệm cận ngang.

Dựa vào bảng biến thiên ta có:
• \(\mathop {\lim }\limits_{x \to - {2^ - }} f\left( x \right) = - \infty \).
Vậy \(x = - 2\) là tiệm cận đứng của đồ thị hàm số đã cho.
• \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = + \infty ;\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = - \infty \).
Vậy hàm số không có tiệm cận ngang.
Chọn A.
