‒ Xét giao điểm của đồ thị hàm số với các trục toạ độ. ‒ Xét các đường tiệm cận của đồ thị hàm số. Hướng dẫn giải Giải bài 74 trang 36 sách bài tập toán 12 - Cánh diều - Bài 4. Khảo sát sự biến thiên và vẽ đồ thị hàm số . Đường cong ở Hình 18 là đồ thị của hàm số: A. \(y = \frac{{{x^2} - 2{\rm{x}}}}{{x - 1}}\). B.
Câu hỏi/bài tập:

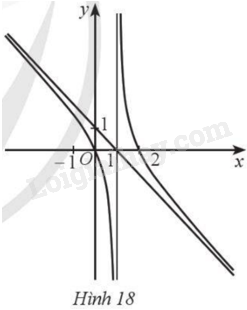
Đường cong ở Hình 18 là đồ thị của hàm số:
A. \(y = \frac{{{x^2} - 2{\rm{x}}}}{{x - 1}}\).
B. \(y = \frac{{{x^2} + 2{\rm{x}}}}{{ - x + 1}}\).
C. \(y = \frac{{ - {x^2} + 2{\rm{x}}}}{{2{\rm{x}} - 2}}\).
D. \(y = \frac{{ - {x^2} + 2{\rm{x}}}}{{x - 1}}\).
Advertisements (Quảng cáo)

‒ Xét giao điểm của đồ thị hàm số với các trục toạ độ.
‒ Xét các đường tiệm cận của đồ thị hàm số.

Đồ thị hàm số đi qua điểm \(\left( {2;0} \right)\). Vậy loại C.
Đồ thị hàm số có tiệm cận xiên là đường thẳng đi qua hai điểm \(\left( {1;0} \right)\) và \(\left( {0;1} \right)\). Vậy \(y = - x + 1\) là tiệm cận xiên của đồ thị hàm số. Vậy loại A, B.
Chọn D.
