‒ Xét giao điểm của đồ thị hàm số với các trục toạ độ. ‒ Xét các đường tiệm cận của đồ thị hàm số. Trả lời Giải bài 75 trang 36 sách bài tập toán 12 - Cánh diều - Bài 4. Khảo sát sự biến thiên và vẽ đồ thị hàm số . Cho hàm số \(y = \frac{{ax + b}}{{cx + d}}\) với \(a > 0\) có đồ thị là đường cong
Câu hỏi/bài tập:

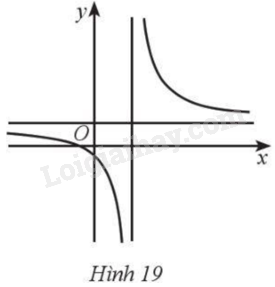
Cho hàm số \(y = \frac{{ax + b}}{{cx + d}}\) với \(a > 0\) có đồ thị là đường cong ở Hình 19. Mệnh đề nào dưới đây đúng?
A. \(b > 0,c < 0,d < 0\).
B. \(b > 0,c > 0,d < 0\).
C. \(b 0,d < 0\).
D. \(b < 0,c < 0,d < 0\).
Advertisements (Quảng cáo)

‒ Xét giao điểm của đồ thị hàm số với các trục toạ độ.
‒ Xét các đường tiệm cận của đồ thị hàm số.

Đồ thị hàm số cắt trục \(Ox\) tại điểm có hoành độ \({x_0} = - \frac{b}{a} 0\). Do \(a > 0\) nên \(b > 0\).
Đồ thị hàm số có tiệm cận ngang là đường thẳng \(y = \frac{a}{c} > 0\). Do \(a > 0\) nên \(c > 0\).
Đồ thị hàm số có tiệm cận đứng là đường thẳng \(x = - \frac{d}{c} > 0 \Leftrightarrow \frac{d}{c} 0\) nên \(d < 0\).
Chọn B.
