Câu hỏi/bài tập:

Cho hàm số \(y = f\left( x \right) = \frac{{a{x^2} + bx + c}}{{mx + n}}\) (với \(a,m \ne 0\)) có đồ thị là đường cong như Hình 23. Căn cứ vào đồ thị hàm số:
a) Tìm khoảng đơn điệu, điểm cực đại, cực tiểu của hàm số.
b) Viết phương trình đường tiệm cận đứng, tiệm cận xiên của đồ thị hàm số.
c) Phương trình \(f\left( x \right) = 3\) có bao nhiêu nghiệm?
d) Tìm công thức xác định hàm số \(y = f\left( x \right)\), biết \(m = 1\).
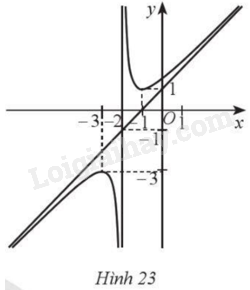

‒ Xét đồ thị hàm số.
‒ Xét các đường tiệm cận của đồ thị hàm số.
‒ Xét các điểm trên đồ thị hàm số.

a) Dựa vào đồ thị hàm số, ta có:
‒ Hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 3} \right)\) và \(\left( { - 1; + \infty } \right)\); nghịch biến trên các khoảng \(\left( { - 3; - 2} \right)\) và \(\left( { - 2; - 1} \right)\).
Advertisements (Quảng cáo)
‒ Hàm số đạt cực đại tại điểm \(x = - 3\), đạt cực tiểu tại điểm \(x = - 1\).
b)
• Tiệm cận đứng của đồ thị hàm số đi qua điểm có hoành độ ‒2.
Vậy \(x = - 2\) là tiệm cận đứng của đồ thị hàm số.
• Tiệm cận xiên của đồ thị hàm số đi qua hai điểm \(\left( { - 1;0} \right)\) và \(\left( { - 2; - 1} \right)\).
Vậy đường thẳng \(y = x + 1\) là tiệm cận xiên của đồ thị hàm số.
c) Đường thẳng \(y = 3\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại 2 điểm. Vậy phương trình \(f\left( x \right) = 3\) có 2 nghiệm.
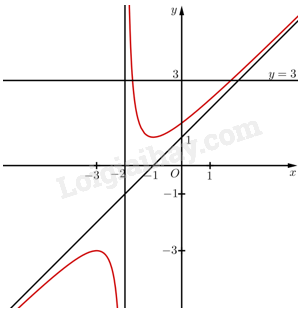
d) Đồ thị hàm số có \(x = - 2\) là tiệm cận đứng. Vậy \( - \frac{n}{m} = - 2 \Leftrightarrow - \frac{n}{1} = - 2 \Leftrightarrow n = 2\).
Tiệm cận xiên của đồ thị hàm số có hệ số góc bằng 1. Vậy \(\frac{a}{m} = 1 \Leftrightarrow \frac{a}{1} = 1 \Leftrightarrow a = 1\).
Đồ thị hàm số đi qua điểm \(\left( { - 1;1} \right)\) nên ta có: \(\frac{{1.{{\left( { - 1} \right)}^2} + b.\left( { - 1} \right) + c}}{{\left( { - 1} \right) + 2}} = 1 \Leftrightarrow - b + c = 0\).
Đồ thị hàm số đi qua điểm \(\left( { - 3; - 3} \right)\) nên ta có: \(\frac{{1.{{\left( { - 3} \right)}^2} + b.\left( { - 3} \right) + c}}{{\left( { - 3} \right) + 2}} = - 3 \Leftrightarrow - 3b + c = - 6\).
Từ đó ta có \(b = 3,c = 3\).
Vậy hàm số cần tìm là: \(y = f\left( x \right) = \frac{{{x^2} + 3{\rm{x}} + 3}}{{{\rm{x}} + 2}}\).
