Dựa vào đồ thị hàm số xác định các cực trị của hàm số. Hướng dẫn giải Giải bài 89 trang 40 sách bài tập toán 12 - Cánh diều - Bài tập cuối chương 1 . Cho hàm số \(y = \frac{{a{x^2} + b{\rm{x}} + c}}{{m{\rm{x}} + n}}\) (với \(a,
Câu hỏi/bài tập:

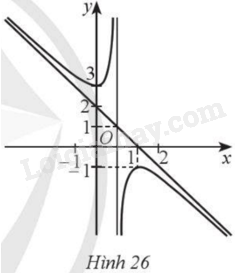
Cho hàm số \(y = \frac{{a{x^2} + b{\rm{x}} + c}}{{m{\rm{x}} + n}}\) (với \(a,m \ne 0\)) có đồ thị là đường cong như Hình 26. Giá trị cực đại của hàm số là:
A. 0.
B. ‒1.
C. 2.
D. 3.
Advertisements (Quảng cáo)

Dựa vào đồ thị hàm số xác định các cực trị của hàm số.

Dựa vào đồ thị ta có: Hàm số đạt cực đại tại \(x = 2\). Khi đó giá trị cực tiểu bằng ‒1.
Chọn B.
