a) Tính thể tích khối nón (H). Đề 1 trang 67 Sách bài tập (SBT) Hình học 12 - ĐỀ KIỂM TRA - CHƯƠNG II
ĐỀ 1 (45 phút)
Câu 1 (4 điểm) trang 67 sách bài tập (SBT) – Hình học 12
Cho hình nón (H) có chiều cao bằng h, đường sinh tạo với mặt phẳng đáy một góc bằng 600.
a) Tính thể tích khối nón (H)
b) Tính thể tích khối cầu nội tiếp hình nón (H).
Hướng dẫn làm bài
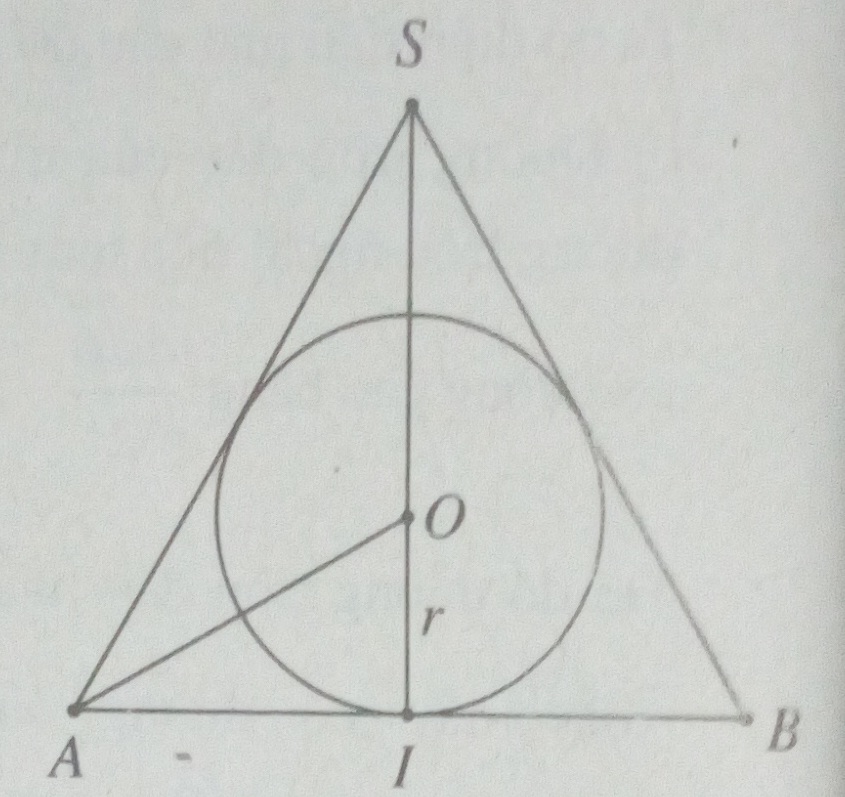
a) Gọi S là đỉnh của hình nón (H), (H’) là hình cầu nội tiếp (H). Mặt phẳng (P) đi qua trục của hình nón (H) cắt (H) theo tam giác cân SAB và cắt hình cầu (H’) theo đường tròn tâm O nội tiếp tam giác SAB. Vì \(\widehat {SAB} = {60^0}\) nên tam giác SAB là tam giác đều. Từ đó suy ra bán kính đường tròn đáy của hình nón (H) bằng:
\(IA = SI.\cot {60^0} = h{{\sqrt 3 } \over 3};{V_{(H)}} = {1 \over 3}\pi {{{h^2}} \over 3}h = {{\pi {h^3}} \over 9}\)
b) Bán kính hình cầu (H’) bằng: \(OI = IA\tan {30^0} = {{h\sqrt 3 } \over 3}.{{\sqrt 3 } \over 3} = {h \over 3}\)
Suy ra: \({V_{(H’)}} = {4 \over 3}\pi {({h \over 3})^3} = {4 \over {81}}\pi {h^3}\)
Câu 2 (6 điểm) trang 67 sách bài tập (SBT) – Hình học 12
Cho tứ diện ABCD có \(AB \bot BC,DA \bot (ABC)\). Gọi M và N theo thứ tự là chân đường vuông góc kẻ từ A đến DB và DC. Biết AB = AD = 4a , BC = 3a.
Advertisements (Quảng cáo)
a) Chứng minh rằng năm điểm A, B, C, M, N cùng nằm trên một mặt cầu (S). Tính thể tích mặt cầu đó.
b) Gọi (S’) là mặt cầu ngoại tiếp tứ diện ADMN. Chứng minh rằng (S) và (S’) giao nhau theo một đường tròn. Tìm bán kính của đường tròn đó.
Hướng dẫn làm bài
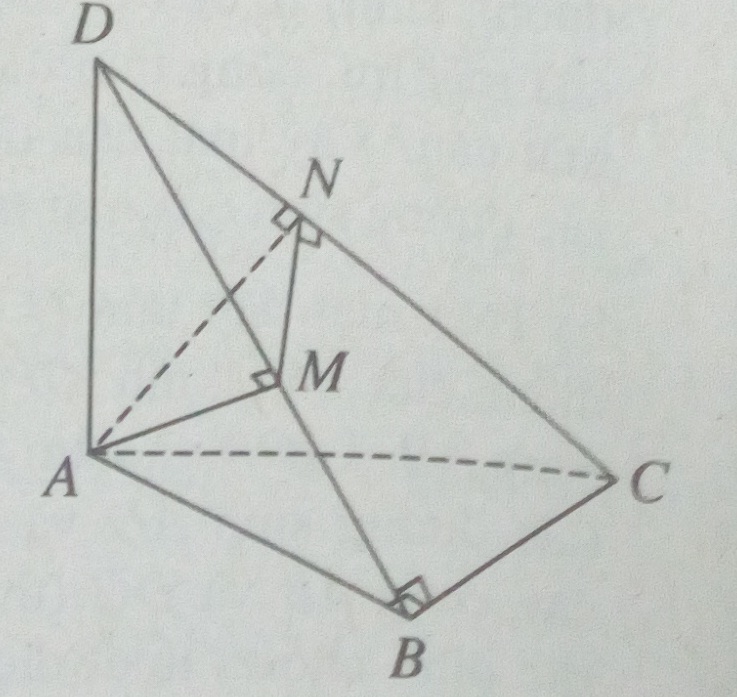
a) Ta có: \(\left\{ {\matrix{{BC \bot AB} \cr {BC \bot AD} \cr} } \right. \Rightarrow BC \bot (ABD)\Rightarrow BC \bot AM\)
\(\left\{ {\matrix{{AM \bot BC} \cr {AM \bot BD} \cr} } \right.\Rightarrow AM \bot (BCD) \Rightarrow AM \bot MC\)
\(\widehat {ABC} = \widehat {AMC} = \widehat {ANC} = {90^0}\) \Rightarrow A, C, B, M, N nằm trên mặt cầu (S) đường kính \(AC = \sqrt {{{(4a)}^2} + {{(3a)}^2}} = 5a\)
b) \(\widehat {AMD} = \widehat {AND} = {90^0}\) => \Rightarrow A, D, M, N nằm trên mặt cầu (S’) đường kính AD.
(S) và(S’) có ba điểm chung là A, M, N.
Ta có: \(\left\{ {\matrix{{AM \bot BC} \cr {AM \bot MC} \cr} \Rightarrow AM \bot (BMC) \Rightarrow AM \bot MN} \right.\)
Từ đó suy ra \((S) \cap (S’)\) theo đường tròn đường kính AN với :
\(AN = {{AD.AC} \over {\sqrt {A{D^2} + A{C^2}} }} = {{4a.5a} \over {\sqrt {16{a^2} + 25{a^2}} }} = {{20a} \over {\sqrt {41} }}\)
Do đó bán kính đường tròn \((S) \cap (S’)\) bằng \({{10\sqrt {41} } \over {41}}a\).
