ĐỀ 2 (45 phút)
Câu 1 (6 điểm) trang 67 sách bài tập (SBT) – Hình học 12
Cho hình trụ (H) có đáy là hai đường tròn tâm O và O’ , bán kính đáy R = OO’. Trên đáy tâm O lấy điểm A, trên đáy tâm O’ lấy điểm B sao cho AB = 2R. Tính tỉ số thể tích giữa khối tứ diện ABOO’ và khối trụ (H).
Hướng dẫn làm bài
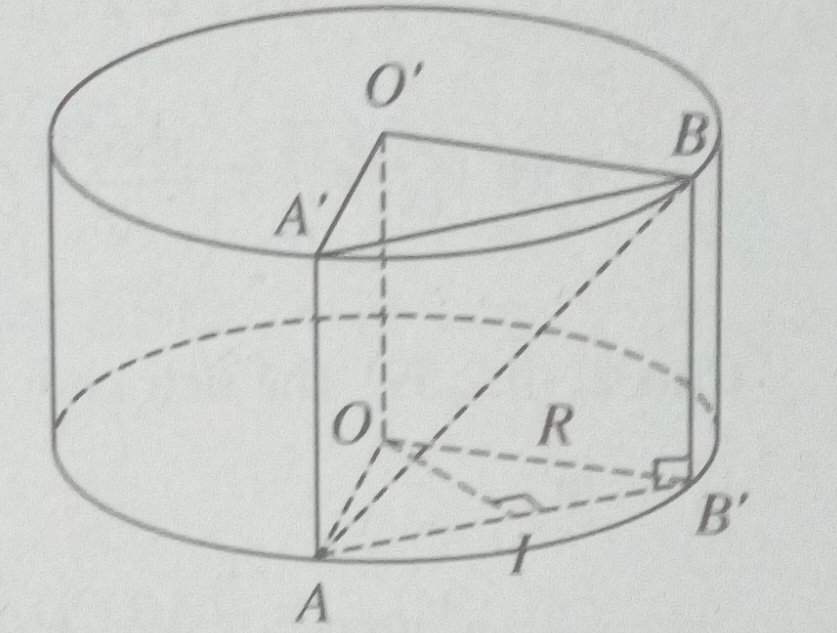
Gọi AA’, BB’ lần lượt là những đường sinh qua A, B của (H). Khi đó, tam giác ABB’ vuông tại B’. Suy ra: \(AB’ = \sqrt {A{B^2} - B'{B^2}} = R\sqrt 3 \) . Gọi I là trung điểm của AB’.
Khi đó \(OI \bot AB’\)
Do đó \(OI = \sqrt {OB{‘^2} - IB{‘^2}} = {R \over 2}\)
\( = > {S_{OAB’}} = {1 \over 2}R\sqrt 3 {R \over 2} = {{{R^2}\sqrt 3 } \over 4}\)
Suy ra: \({V_{ABOO’}} = {V_{B.AOO’}} = {V_{B.{\rm{AA}}’O’}} = {V_{A.A’BO’}} = {1 \over 3}{V_{OAB’.O’A’B}}\)
\(= {1 \over 3}{{{R^2}\sqrt 3 } \over 4}R = {{\sqrt 3 {R^3}} \over {12}}\);
Advertisements (Quảng cáo)
\({V_{(H)}} = \pi {R^3}\)
Vậy \({{{V_{ABOO’}}} \over {{V_{(H)}}}} = {{\sqrt 3 } \over {12\pi }}\)
Câu 2 (4 điểm) trang 67 sách bài tập (SBT) – Hình học 12
a) Cho hình hộp chữ nhật có ba kích thước là x, y, z. Tính thể tích hình cầu (S) ngoại tiếp hình hộp chữ nhật đó.
b) Trong số những hình hộp chữ nhật nội tiếp hình cầu (S) cho trước hình hộp nào có thể tích lớn nhất.
Hướng dẫn làm bài
a) Hình cầu đó có tâm là giao của các đường chéo của hình hộp chữ nhật, nên bán kính của (S) là \({1 \over 2}\sqrt {{x^2} + {y^2} + {z^2}} \) . Thế tích \({V_{(S)}} = {4 \over 3}\pi {({x^2} + {y^2} + {z^2})^{{3 \over 2}}}\)
b) Thể tích của hình hộp bằng V = xyz. Gọi R là bán kính hình cầu (S). Ta có: \(\root 3 \of {{x^2}{y^2}{z^2}} \le {{{x^2} + {y^2} + {z^2}} \over 3} = {{4{R^2}} \over 3}\)
Suy ra V lớn nhất <=> V2 = x2 y2 z2 lớn nhất
<=> x2 = y2 = z2 <=> x = y = z
Do đó trong số những hình hộp chữ nhật nội tiếp hình cầu (S) cho trước, hình lập phương là hình có thể tích lớn nhất.
