ĐỀ 3.
Câu 1 trang 225 sách bài tập (SBT) – Giải tích 12 (4 điểm)
Cho hàm số: \(y = - {x^3} + 3x - 2\)
1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.
2) Viết phương trình tiếp tuyến của (C) tại điểm M(1; 0).
3) Biện luận theo m số nghiệm của phương trình \( - {x^3} + 3x - 2 = {\log _3}m\)
Hướng dẫn làm bài
1) Vẽ biểu đồ
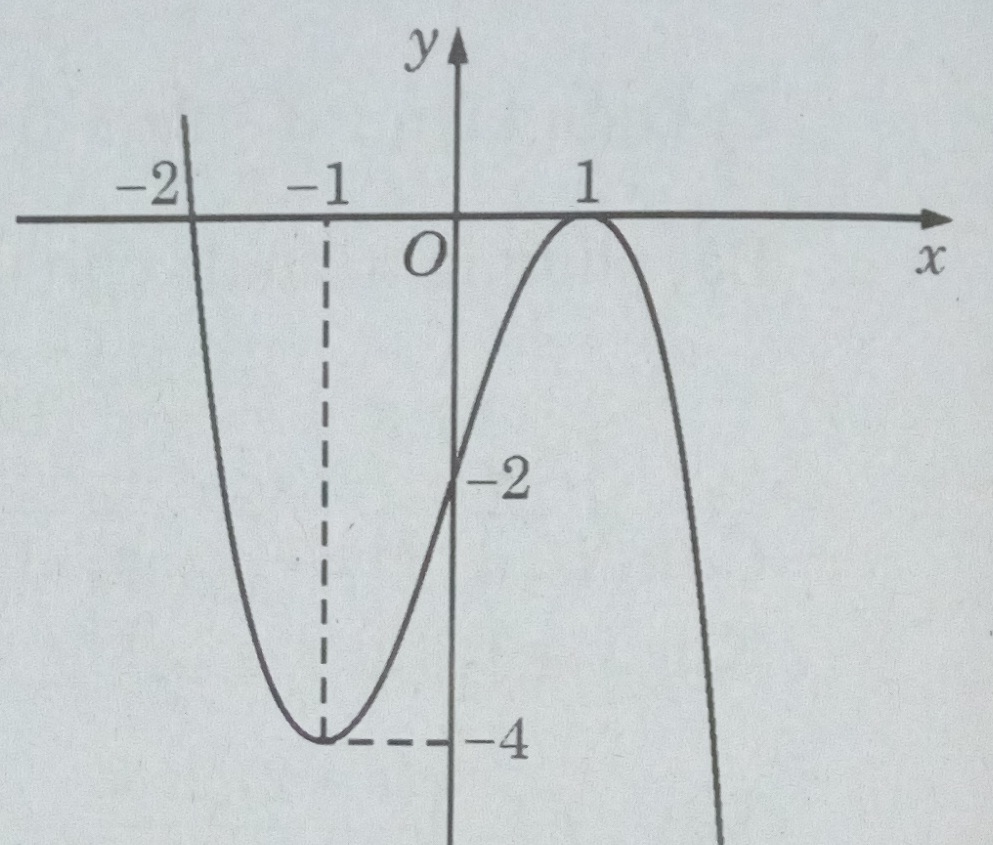
2) Ta có: y’(1) = 0. Vậy phương trình của tiếp tuyến là y = 0
3) Dựa vào đồ thị (C) và đường thẳng \(y = {\log _3}m\) , ta có:
* Khi \({\log _3}m < - 4 \Leftrightarrow m < {1 \over {81}}\), phương trình có một nghiệm
* Khi \({\log _3}m = - 4 \Leftrightarrow m = {1 \over {81}}\), phương trình có hai nghiệm.
* Khi \(0 > {\log _3}m > - 4 \Leftrightarrow 1 > m > {1 \over {81}}\), phương trình có ba nghiệm.
* Khi \({\log _3}m = 0 \Leftrightarrow m = 1\), phương trình có hai nghiệm.
* Khi \({\log _3}m > 0 \Leftrightarrow m > 1\) , phương trình có một nghiệm.
Kết luận:
* Phương trình có một nghiệm khi m > 1 hoặc \(m < {1 \over {81}}\)
* Phương trình có hai nghiệm khi m = 1 hoặc \(m = {1 \over {81}}\)
* Phương trình có ba nghiệm khi \({1 \over {81}} < m < 1\) .
Câu 2 trang 225 sách bài tập (SBT) – Giải tích 12 (3 điểm)
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số:
Advertisements (Quảng cáo)
1) \(f(x) = \ln ({x^2} + x - 2)\) trên đoạn [3; 6]
2) \(f(x) = {\cos ^2}x + \cos x + 3\)
Hướng dẫn làm bài
1) f(x) xác định trên R\[-2; 1] nên xác định trên đoạn [3; 6]
\(f'(x) = {{2x + 1} \over {{x^2} + x - 2}}\)
Ta thấy \(f{\rm{ }}\left( x \right){\rm{ }} > {\rm{ }}0{\rm{ }},\forall x \in {\rm{[}}3;6]\) nên trên đoạn [3; 6] hàm số f(x) đồng biến.
Vậy \(\mathop {\min }\limits_{{\rm{[}}3;6]} f(x) = f(3) = \ln 10;\mathop {\max }\limits_{{\rm{[}}3;6]} f(x) = f(6) = \ln 40\)
2) Vì f(x) là hàm số tuần hoàn chu kì \(2\pi \), nên ta chỉ cần xét f(x) trên đoạn \({\rm{[}}0;2\pi {\rm{]}}\)
\(f'(x) = - 2\sin x\cos x - \sin x;f'(0) = 0 \Leftrightarrow x = {\rm{\{ }}0;{{2\pi } \over 3};\pi ;{{4\pi } \over 3};2\pi {\rm{\} }}\)
\(f(0) = f(2\pi ) = 5;f({{2\pi } \over 3}) = 2{3 \over 4};f(\pi ) = 3;f({{4\pi } \over 3}) = 2{3 \over 4}\)
Vậy \(\mathop {\min }\limits_R f(x) = \mathop {\min }\limits_{{\rm{[}}0;2\pi {\rm{]}}} f(x) = 2{3 \over 4};\mathop {\max }\limits_R f(x) = \mathop {\max }\limits_{{\rm{[}}0;2\pi {\rm{]}}} f(x) = 5\)
Câu 3 trang 226 sách bài tập (SBT) – Giải tích 12 (3 điểm)
1) Tính các tích phân sau:
a) \(\int\limits_0^1 {(3{x^2} + 2x + 1){e^{2x}}dx}\) b) \(\int\limits_0^{{\pi \over 2}} {\cos 3x} .\cos 4xdx\)
2) Tìm modun của các số phức sau:
a) \(z = ( - 4 + i\sqrt {48} )(2 + i)\) b) \(z = {{1 + i} \over {2 - i}}\)
Hướng dẫn làm bài
1) a) Đáp số : \({7 \over 4}{e^2} - {3 \over 4}\)
b) \(\int\limits_0^{{\pi \over 2}} {\cos 3x\cos 4xdx} = {1 \over 2}\int\limits_0^{{\pi \over 2}} {(\cos 7x + \cos x)dx = {3 \over 7}} \)
2) a) \(z = ( - 4 + i\sqrt {48} )(2 + i)\) nên
\(|z| = | - 4 + i\sqrt {48} |.|2 + i| = \sqrt {{{( - 4)}^2} + {{(\sqrt {48} )}^2}} .\sqrt {{2^2} + {1^2}} = 8\sqrt 5 \)
b) \(z = {{1 + i} \over {2 - i}}\) nên \(|z| = {{|1 + i|} \over {|2 - i|}} = {{\sqrt 2 } \over {\sqrt {{2^2} + {{( - 1)}^2}} }} = \sqrt {{2 \over 5}} \).
