Hoạt động3
Trả lời câu hỏi Hoạt động 3 trang 9
Dựa vào đồ thị hàm số \(y = f\left( x \right) = - {x^3} - 3{x^2} + 3\) ở Hình 3, hãy so sánh:
a) \(f\left( { - 2} \right)\) với mỗi giá trị \(f\left( x \right)\), ở đó \(x \in \left( { - 3; - 1} \right)\) và \(x \ne - 2\).
b) \(f\left( 0 \right)\)với mỗi giá trị \(f\left( x \right)\), ở đó \(x \in \left( { - 1;1} \right)\) và \(x \ne 0\).
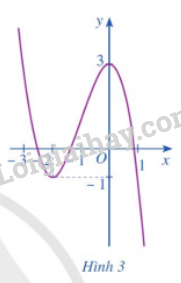

Dựa vào đồ thị hàm số

a) Nhận xét: Ta thấy rằng \(f\left( x \right) > f\left( { - 2} \right)\) với mọi \(x \in \left( { - 3; - 1} \right)\) và \(x \ne - 2\).
b) Tương tự: Ta thấy rằng \(f\left( x \right) < f\left( 0 \right)\) với mọi \(x \in \left( { - 1;1} \right)\) và \(x \ne 0\).
Hoạt động4
Trả lời câu hỏi Hoạt động 4 trang 10
Quan sát bảng biến thiên dưới đây và cho biết:
a) \({x_o}\) có là điểm cực đại của hàm số \(f\left( x \right)\) hay không.
b) \({x_1}\) có là điểm cực tiểu của hàm số \(h\left( x \right)\) hay không.


Dựa vào Bảng biến thiên và định nghĩa điểm cực tiểu của hàm số

a) \({x_o}\) có là điểm cực đại của hàm số \(f\left( x \right)\) .
b) \({x_1}\) có là điểm cực tiểu của hàm số \(h\left( x \right)\).
Luyện tập5
Advertisements (Quảng cáo)
Trả lời câu hỏi Luyện tập 5 trang 11
Tìm điểm cực trị của mỗi hàm số sau:
a) \(y = {x^4} - 6{x^2} + 8x + 1\).
b) \(y = \frac{{3x + 5}}{{x - 1}}\).

B1: Tìm tập xác định của hàm số.
B2: Tính đạo hàm. Tìm các điểm mà tại đó đạo hàm bằng không hoặc không tồn tại.
B3: Lập bảng biến thiên.
B4: Dựa vào bảng biến thiên để kết luận.

a) Tập xác định: \(D = \mathbb{R}\).
Ta có: \(y’ = 4{x^3} - 12x + 8\).
Xét \(y’ = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 2\\x = 1\end{array} \right.\)
Ta có bảng biến thiên sau:
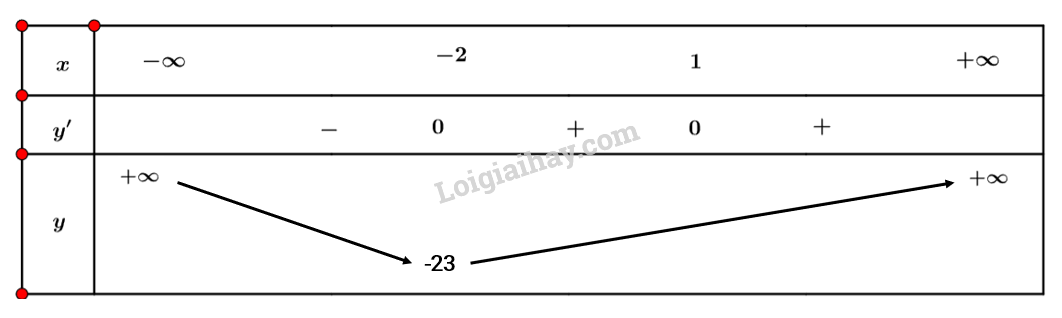
Vậy hàm số đạt cực đại tại điểm \(x = - 2\).
b) Tập xác định: \(D = \mathbb{R}\backslash \left\{ 1 \right\}\).
Ta có: \(y’ = \frac{{ - 8}}{{{{\left( {x - 1} \right)}^2}}}\).
Nhận xét \(y’ < 0{\rm{ }}\forall x \in D\)
Ta có bảng biến thiên sau:
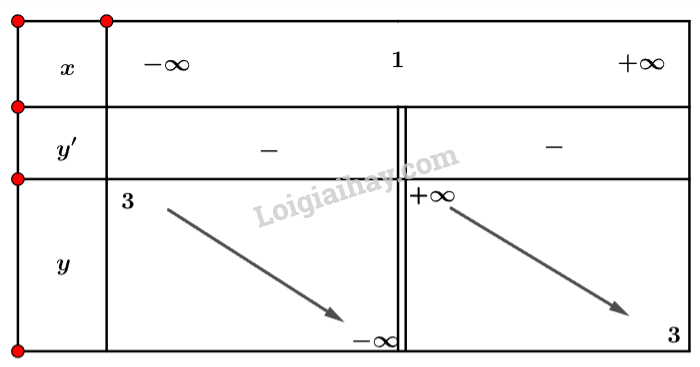
Vậy hàm số không có điểm cực trị.
