Câu hỏi/bài tập:
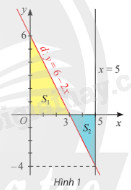
Gọi \(d\) là đồ thị của hàm số \(y = f\left( x \right) = 6 - 2x\). Kí hiệu \({S_1}\) là diện tích hình phẳng giới hạn bởi \(d\), trục hoành và trục tung; \({S_2}\) là diện tích hình phẳng giới hạn bởi \(d\), trục hoành và đường thẳng \(x = 5\) (Hình 1).
a) Tính \({S_1}\) và so sánh với \(\int\limits_0^3 {f\left( x \right)dx} \).
b) Tính \({S_2}\) và so sánh với \(\int\limits_3^5 {f\left( x \right)dx} \).
c) So sánh \(\int\limits_0^5 {\left| {f\left( x \right)} \right|dx} \) với \({S_1} + {S_2}\).

a) Theo hình vẽ, \({S_1}\) là diện tích tam giác \(OAB\). Tính diện tích tam giác \(OAB\), sau đó tính tích phân \(\int\limits_0^3 {f\left( x \right)dx} \) và so sánh các kết quả thu được.
b) Theo hình vẽ. \({S_2}\) là diện tích tam giác \(CBM\). Tính diện tích tam giác \(CBM\), sau đó tính tích phân \(\int\limits_3^5 {f\left( x \right)dx} \) và so sánh các kết quả thu được.
c) Tính \(\int\limits_0^5 {\left| {f\left( x \right)} \right|dx} = \int\limits_0^3 {\left| {f\left( x \right)} \right|dx} + \int\limits_3^5 {\left| {f\left( x \right)} \right|dx} \), sau đó phá dấu giá trị tuyệt đối và tính các tích phân cơ bản, sau đó so sánh kết quả thu được với \({S_1} + {S_2}\).

a) Tam giác \(OAB\) vuông tại \(O\), ta có \(OA = 6\), \(OB = 3\). Diện tích tam giác \(OAB\) là:
Advertisements (Quảng cáo)
\({S_1} = \frac{{OA.OB}}{2} = \frac{{6.3}}{2} = 9\).
Ta có \(\int\limits_0^3 {f\left( x \right)dx} = \int\limits_0^3 {\left( {6 - 2x} \right)dx} = \left. {\left( {6x - {x^2}} \right)} \right|_0^3 = 9 - 0 = 9\).
Như vậy \({S_1} = \int\limits_0^3 {f\left( x \right)dx} \)
b) Tam giác \(CBM\) vuông tại \(M\), ta có \(MB = 2\), \(MC = 4\). Diện tích tam giác \(CBM\) là:
\({S_2} = \frac{{MB.MC}}{2} = \frac{{2.4}}{2} = 4\).
Ta có \(\int\limits_0^3 {f\left( x \right)dx} = \int\limits_3^5 {\left( {6 - 2x} \right)dx} = \left. {\left( {6x - {x^2}} \right)} \right|_3^5 = 5 - 9 = - 4\).
Như vậy \({S_2} = - \int\limits_3^5 {f\left( x \right)dx} \)
c) Ta có:
\(\int\limits_0^5 {\left| {f\left( x \right)} \right|dx} = \int\limits_0^5 {\left| {6 - 2x} \right|dx} = \int\limits_0^3 {\left| {6 - 2x} \right|dx} + \int\limits_3^5 {\left| {6 - 2x} \right|dx} = \int\limits_0^3 {\left( {6 - 2x} \right)dx} + \int\limits_3^5 {\left( {2x - 6} \right)dx} \)
\( = \left. {\left( {6x - {x^2}} \right)} \right|_0^3 + \left. {\left( {{x^2} - 6x} \right)} \right|_3^5 = \left( {9 - 0} \right) + \left[ {\left( { - 5} \right) - \left( { - 9} \right)} \right] = 13\)
Như vậy \(\int\limits_0^5 {\left| {f\left( x \right)} \right|dx} = 13 = {S_1} + {S_2}\).
