Câu hỏi/bài tập:
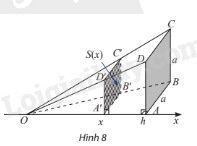
Trong không gian, cho hình chóp \(O.ABCD\) có đáy là hình vuông cạnh \(a\), \(OA \bot \left( {ABCD} \right)\), \(OA = h\). Đặt trục số \(Ox\) như hình 8. Một mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\) \(\left( {0 < x \le h} \right)\), cắt hình chóp \(O.ABCD\) theo mặt cắt là hình vuông \(A'B'C'D'\). Kí hiệu \(S\left( x \right)\) là diện tích của hình vuông \(A'B'C'D'\).
a) Tính \(S\left( x \right)\) theo \(a\), \(h\) và \(x\).
b) Tính \(\int\limits_0^h {S\left( x \right)dx} \) và so sánh với thể tích của khối chóp \(O.ABCD\).

a) Do \(A’B’C’D’\) là hình vuông, nên \(S\left( x \right) = A’D{‘^2}\)
Tam giác \(OAD\) có \(AD\parallel A’D’\) nên \(\frac{{OA’}}{{OA}} = \frac{{A’D’}}{{AD}}\), từ đó tính được \(A’D’\), sau đó tính \(S\left( x \right)\).
Advertisements (Quảng cáo)
b) Tính \(\int\limits_0^h {S\left( x \right)dx} \) và thể tích khối chóp \(O.ABCD\) và so sánh các kết quả với nhau.

a) Do \(A’B’C’D’\) là hình vuông, nên \(S\left( x \right) = A’D{‘^2}\)
Tam giác \(OAD\) có \(AD\parallel A’D’\) nên \(\frac{{OA’}}{{OA}} = \frac{{A’D’}}{{AD}} \Rightarrow A’D’ = \frac{{OA’.AD}}{{OA}} = \frac{{x.a}}{h}\)
Suy ra \(S\left( x \right) = A’D{‘^2} = {\left( {\frac{{x.a}}{h}} \right)^2} = \frac{{{a^2}}}{{{h^2}}}{x^2}\)
b) Ta có: \(\int\limits_0^h {S\left( x \right)dx} = \frac{{{a^2}}}{{{h^2}}}\int\limits_0^h {{x^2}dx} = \frac{{{a^2}}}{{{h^2}}}\left. {\left( {\frac{{{x^3}}}{3}} \right)} \right|_0^h = \frac{{{a^2}}}{{{h^2}}}.\frac{{{h^3}}}{3} = \frac{{{a^2}h}}{3}\)
Thể tích khối chóp \(O.ABCD\) là \({V_{O.ABCD}} = \frac{1}{3}.{a^2}.h = \frac{{{a^2}h}}{3}\)
Như vậy \({V_{O.ABCD}} = \int\limits_0^h {S\left( x \right)dx} \)
