Câu hỏi/bài tập:
Một bình chứa nước có dạng như hình 11. Biết rằng khi nước ở trong bình có chiều cao \(x\) (dm) \(\left( {0 \le x \le 4} \right)\) thì mặt nước là hình vuông có cạnh \(\sqrt {2 + \frac{{{x^2}}}{4}} \) (dm). Tính dung tích của bình.
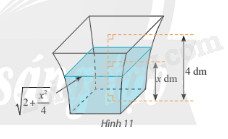

Chọn trục \(Ox\) vuông góc với mặt đáy của bình sao cho đáy nhỏ, đáy to của bình vuông góc với \(Ox\) lần lượt tại \(x = 0\) và \(x = 4\)
Diện tích mặt nước ở chiều cao \(x\) là \(S\left( x \right) = {\left( {\sqrt {2 + \frac{{{x^2}}}{4}} } \right)^2} = 2 + \frac{{{x^2}}}{4}\)
Advertisements (Quảng cáo)
Dung tích của bình là \(V = \int\limits_0^4 {S\left( x \right)dx} \)

Chọn trục \(Ox\) vuông góc với mặt đáy của bình sao cho đáy nhỏ, đáy to của bình vuông góc với \(Ox\) lần lượt tại \(x = 0\) và \(x = 4\)
Diện tích mặt nước ở chiều cao \(x\) là \(S\left( x \right) = {\left( {\sqrt {2 + \frac{{{x^2}}}{4}} } \right)^2} = 2 + \frac{{{x^2}}}{4}\)
Dung tích của bình là \(V = \int\limits_0^4 {S\left( x \right)dx} = \int\limits_0^4 {\left( {2 + \frac{{{x^2}}}{4}} \right)dx} = \left. {\left( {2x + \frac{{{x^3}}}{{12}}} \right)} \right|_0^4 = \frac{{40}}{3}\)
