Câu hỏi/bài tập:

Cho tứ diện ABCD, gọi G là trọng tâm của tam giác BCD và M là trung điểm của đoạn thẳng AG. Khi đó \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} \) bằng
A. \(\overrightarrow {MG} \).
B. \(2\overrightarrow {MG} \).
C. \(3\overrightarrow {MG} \).
D. \(4\overrightarrow {MG} \).

Sử dụng kiến thức về quy tắc ba điểm để tính: Nếu A, B, C là ba điểm bất kì thì \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Advertisements (Quảng cáo)
Sử dụng kiến thức về hệ thức vectơ về trọng tâm của tam giác để tính: Nếu G là trọng tâm của tam giác ABC thì \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)

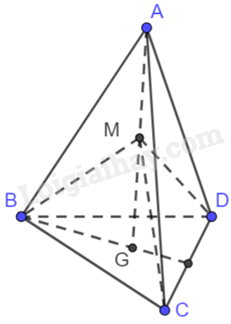
Vì M là trung điểm của AG nên \(\overrightarrow {MA} = - \overrightarrow {MG} \).
Vì G là trọng tâm của tam giác BCD nên \(\overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \)
Ta có: \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = - \overrightarrow {MG} + \overrightarrow {MG} + \overrightarrow {GB} + \overrightarrow {MG} + \overrightarrow {GC} + \overrightarrow {MG} + \overrightarrow {GD} \)
\( = 2\overrightarrow {MG} + \left( {\overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} } \right) = 2\overrightarrow {MG} \)
Chọn B
