Bài 9. Tìm diện tích mặt cầu ngoại tiếp hình chóp S.ABC biết rằng SA = a, SB = b, SC = c và ba cạnh SA, SB, SC đôi một vuông góc. Chứng minh rằng các điểm S, trọng tâm tam giác ABC và tâm mặt cầu ngoại tiếp hình chóp S.ABC thẳng hàng.

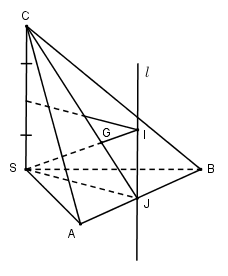
Gọi J là trung điểm của AB và \(l \) là đường thẳng qua J vuông góc với mp(SAB) thì \(l\) là trục của tam giác SAB (mọi điểm trên \(l \) đều cách đều S, A, B).
Gọi I là giao điểm của \(l\) với mặt phẳng trung trực đoạn CS thì I cách đều bốn điểm S, A, B, C. Mặt cầu ngoại tiếp hình chóp SABC có tâm I và bán kính R = IA. Ta có:
Advertisements (Quảng cáo)
\({R^2} = I{A^2} = A{J^2} + I{J^2} = {\left( {{{AB} \over 2}} \right)^2} + {\left( {{{SC} \over 2}} \right)^2} = {1 \over 4}\left( {{a^2} + {b^2} + {c^2}} \right)\)
Diện tích mặt cầu là \(S = 4\pi {R^2} = \pi \left( {{a^2} + {b^2} + {c^2}} \right)\)
Vì \(SC // l \) nên SI cắt CJ tại G và \({{GJ} \over {GC}} = {{IJ} \over {SC}} = {1 \over 2}\) nên G là trọng tâm tam giác ABC. Vậy S, G và tâm mặt cầu ngoại tiếp hình chóp S.ABC thẳng hàng.
