Advertisements (Quảng cáo)
Cho hình chóp S.ABC. Biết rằng có một mặt cầu tiếp xúc với ba cạnh của tam giác ABC tại trung điểm của mỗi cạnh, đồng thời mặt cầu đó đi qua trung điểm của các cạnh SA, SB, SC.
1) Chứng minh rằng S.ABC là hình chóp đều.
2) Tính diện tích mặt cầu, biết cạnh đáy và chiều cao của hình chóp lần lượt là a và h.
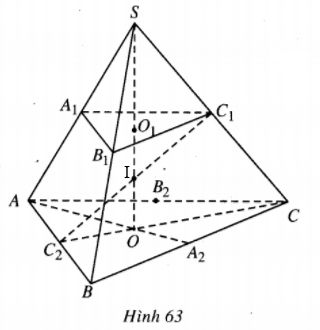
1) Gọi \({A_1},{B_1},{C_1}\) lần lượt là trung điểm của SA, SB, SC và \({A_2},{B_2},{C_2}\) lần lượt là trung điểm của BC, CA, AB. Vì AB, AC là hai tiếp tuyến với mặt cầu tại \({B_2},{C_2}\) nên \(A{B_2} = A{C_2}\), suy ra AB = AC.
Tương tự ta có BA = BC.
Vậy AB = AC = BC, nghĩa là ABC là tam giác đều.
Advertisements (Quảng cáo)
Gọi O là tâm của tam giác đều ABC thì O cũng là tâm của tam giác đều \({A_2}{B_2}{C_2}\).
Kí hiệu O1 là giao điểm của SO và \(mp({A_1}{B_1}{C_1})\) thì O1 cũng là tâm của tam giác đều \({A_1}{B_1}{C_1}\) (vì phép vị tự tâm S, tỉ số \({1 \over 2}\) biến tam giác ABC thành tam giác \({A_1}{B_1}{C_1}\)). Do mp(\({A_1}{B_1}{C_1}\)) song song với mp(ABC) nên \({O_1}O\) đi qua tâm I của mặt cầu, đồng thời \({O_1}O\) vuông góc với cả hai mặt phẳng đó, từ đó SA=SB=SC.
Vậy S.ABC là hình chóp đều.
2) Dễ thấy tâm I của mặt cầu là trung điểm của \({O_1}O\) và bán kính r của mặt cầu bằng \(I{C_2}\). Ta có \(IC_2^2 = I{O^2} + OC_2^2 = {{{h^2}} \over {16}} + {{{a^2}} \over {12}}.\)
Vậy diện tích mặt cầu đó bằng
\(4\left( {{{{h^2}} \over {16}} + {{{a^2}} \over {12}}} \right)\pi = \pi \left( {{{{h^2}} \over 4} + {{{a^2}} \over 3}} \right).\)