Bài 2 trang 50 SGK Hình học 12: Ôn tập chương II - Mặt nón mặt trụ mặt cầu. Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC) và cạnh BD vuông góc với cạnh BC. Biết AB = AD = a, tính diện tích xung quanh và thể tích của khối nón được tạo thành khi quay đường gấp khúc BDA quanh cạnh AB.
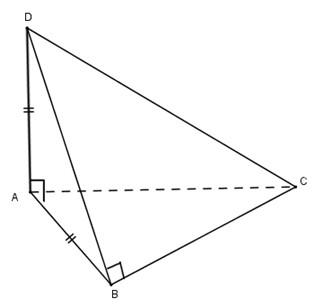
Bài 2. Cho tứ diện \(ABCD\) có cạnh \(AD\) vuông góc với mặt phẳng \((ABC)\) và cạnh \(BD\) vuông góc với cạnh \(BC\). Biết \(AB = AD = a\), tính diện tích xung quanh và thể tích của khối nón được tạo thành khi quay đường gấp khúc \(BDA\) quanh cạnh \(AB\).

Advertisements (Quảng cáo)
Vì \(∆ABD\) vuông góc tại \(A\), nên khi quay \(BDA\) quanh \(AB\) ta được hình nón tròn xoay đường cao \(AB = a\) và bán kính đáy bằng \(AD = r =a\).
Vậy \(V\)nón = \({1 \over 3}\pi {r^2}h = {1 \over 3}\pi {a^3}\)
\(S\)xq = \(πrl\) ở đó đường sinh \(l = a\sqrt2\) nên \(S\)xq = \(\sqrt2πa^2\).
