Bài 3. Hình chóp \(S.ABC\) có đáy là tam giác \(ABC\) vuông tại \(A\), có \(SA\) vuông góc với mặt phẳng \((ABC)\) và có \(SA = a, AB = b, AC = c\). Mặt cầu đi qua các đỉnh \(A, B, C, S\) có bán kính \(r\) bằng:
(A) \({{2(a + b + c)} \over 3}\) ; (B) 2\(\sqrt {{a^2} + {b^2} + {c^2}} \) ;
(C) \({1 \over 2}\sqrt {{a^2} + {b^2} + {c^2}} \) ; (D) \(\sqrt {{a^2} + {b^2} + {c^2}} \) .

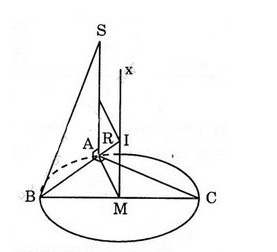
Tâm \(I\) của mặt cầu đi qua \(A,B,C,S\) là giao của trục đường tròn ngoại tiếp tam giác \(ABC\) và mặt phẳng trung trực của \(SA\)
Advertisements (Quảng cáo)
Tam giác \(ABC\) vuông tại \(A\) nên trục đường tròn \(Mx\) với \(M\) là trung điểm của \(BC\).
Bán kính mặt cầu \(R=IA\)
\(MI={a\over 2}\), \(AM={1\over 2} BC\)
\(BC=\sqrt{b^2+c^2}\)
Do đó \(R={1 \over 2}\sqrt {{a^2} + {b^2} + {c^2}} \)
Chọn (C) \({1 \over 2}\sqrt {{a^2} + {b^2} + {c^2}} \)
