Bài 6. Cho hình vuông \(ABCD\) cạnh \(a\). Từ tâm \(O\) của hình vuông dựng đường thẳng \(\Delta\) vuông góc với mặt phẳng \((ABCD)\). Trên \(\Delta\) lấy điểm \(S\) sao cho \(OS ={a \over 2}\). Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp \(S.ABCD\). Tính diện tích của mặt cầu và thể tích của khối cầu được tạo nên bởi mặt cầu đó.

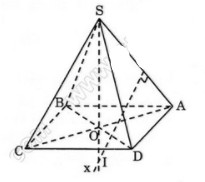
Do \(\Delta\) là trục của hình vuông \(ABCD\), nên tâm \(I\) của mặt cầu ngoại tiếp hình chóp \(S.ABCD\) nằm trên \(\Delta\).
Vì \(SO = {a \over 2} < OC = {{a\sqrt 2 } \over 2}\) nên tâm \(I\) của mặt cầu nằm trên phần kéo dài của \(SO\).
Ta có: \(SI = IC \Rightarrow {a \over 2} + OI = \sqrt {O{I^2} + O{C^2}} \)
Advertisements (Quảng cáo)
\( \Rightarrow {\left( {{a \over 2} + OI} \right)^2} = O{I^2} + {{{a^2}} \over 2}\)
\( \Rightarrow O{I^2} + a.OI + {{{a^2}} \over 4} = O{I^2} + {{{a^2}} \over 4}\)
\( \Rightarrow OI = {a \over 4} \Rightarrow R = SO + OI = {{3a} \over 4}\)
Vậy tâm \(I\) của mặt cầu ngoại tiếp hình chóp \(S.ABCD\) nằm trên \(SO\) mà \(SI = R =\) \({{3a} \over 4}\) ; (\(R\) là bán kính hình cầu). Khi đó diện tích mặt cầu là:
\(S = 4\pi {R^2} = {9 \over 4}\pi {a^2}\) (đvdt)
Thể tích của khối cầu là: \(V = {4 \over 3}\pi {R^3} = {9 \over {16}}{\pi ^3}\) (đvdt)
