Bài 3. Trong không gian \(Oxyz\) cho ba vectơ
\(\overrightarrow a = ( - 1;1;0)\), \(\overrightarrow b = (1;1;0)\) và \(\overrightarrow c = (1;1;1)\)
Cho hình bình hành \(OADB\) có \(\overrightarrow {OA} \) = \(\overrightarrow a \), \(\overrightarrow {OB} = \overrightarrow b \) (\(O\) là gốc toạ độ). Toạ độ của tâm hình bình hành \(OADB\) là:
(A) \((0 ; 1 ; 0)\) (B) \((1 ; 0 ; 0)\)
(C) \((1 ; 0 ; 1)\) (D) \((1 ; 1 ; 0)\).

Advertisements (Quảng cáo)
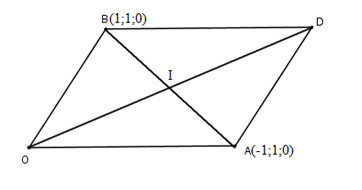
Gọi tọa độ của \(D(x;y;z)\)
\(OADB\) là hình bình hành nên \(\overrightarrow {OD} = \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow a + \overrightarrow b=(0;2;0) \)
Gọi \(I\) là tâm của hình bình hành nên \(\vec{OI}={1\over2}\vec{OD}=(0;1;0)\)
Vậy \(I(0;1;0)\)
Chọn (A) \((0 ; 1 ; 0)\).
