1. Tính (theo mẫu)
Mẫu: \({3 \over 7} \times 4 = {{3 \times 4} \over 7} = {{12} \over 7}\)
a) \({5 \over {11}} \times 7\) b) \({{21} \over 5} \times 1\) c) \({5 \over 6} \times 0\)
2. Tính (theo mẫu):
Mẫu: \(3 \times {5 \over 8} = {{3 \times 5} \over 8} = {{15} \over 8}\)
a) \(4 \times {5 \over {11}}\) b) \(1 \times {{51} \over 4}\) c) \(0 \times {{12} \over 5}\)
3. Tính rồi so sánh kết quả của \({1 \over 5} \times 3\) và \({1 \over 5} + {1 \over 5} + {1 \over 5}\)
\({1 \over 5} \times 3 = \....\) \({1 \over 5} + {1 \over 5} + {1 \over 5} = \....\)
Vậy \({1 \over 5} \times 3\....{1 \over 5} + {1 \over 5} + {1 \over 5}\)
4. Tính (theo mẫu):
Mẫu: \({5 \over 7} \times {9 \over 5} = {{5 \times 9} \over {7 \times 5}} = {9 \over 7}\)
a) \({3 \over 8} \times {8 \over 7}\) b) \({{13} \over 7} \times {7 \over {13}}\)
5.Tính chu vi và diện tích hình vuông có cạnh \({3 \over 8}\) m

1.
a) \({5 \over {11}} \times 7 = {{5 \times 7} \over {11}} = {{35} \over {11}}\)
b) \({{21} \over 5} \times 1 = {{21 \times 1} \over 5} = {{21} \over 5}\)
c) \({5 \over 6} \times 0 = {{5 \times 0} \over 6} = 0\)
Advertisements (Quảng cáo)
2.
a) \(4 \times {5 \over {11}} = {{4 \times 5} \over {11}} = {{20} \over {11}}\)
b) \(1 \times {{51} \over 4} = {{1 \times 51} \over 4} = {{51} \over 4}\)
c) \(0 \times {{12} \over 5} = {{0 \times 12} \over 5} = 0\)
3.
\({1 \over 5} \times 3 = {{1 \times 3} \over 5} = {3 \over 5}\,\,;\,\,{1 \over 5} + {1 \over 5} + {1 \over 5} = {{1 + 1 + 1} \over 5} = {3 \over 5}\)
Vậy \({1 \over 5} \times 3 = {1 \over 5} + {1 \over 5} + {1 \over 5}\)
4.
Mẫu: \({5 \over 7} \times {9 \over 5} = {{5 \times 9} \over {7 \times 5}} = {9 \over 7}\)
a) \({3 \over 8} \times {8 \over 7} = {{3 \times 8} \over {8 \times 7}} = {3 \over 7}\)
b) \({{13} \over 7} \times {7 \over {13}} = {{13 \times 7} \over {7 \times 13}} = 1\)
5. Tóm tắt
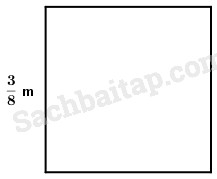
Bài giải
Chu vi hình vuông là: \({3 \over 8} \times 4 = {3 \over 2}\,\,\left( m \right)\)
Diện tích hình vuông là: \({3 \over 8} \times {3 \over 8} = {9 \over {64}}\,\,\left( {{m^2}} \right)\)
Đáp số: \({3 \over 2}m;{9 \over {64}}{m^2}\)
