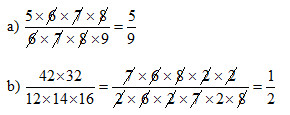1. Điền dấu (>,=,<) vào chỗ chấm.
a) \({6 \over {11}}...{8 \over {11}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{9 \over {15}}...{6 \over {10}}\)
b) \({8 \over 5}...{8 \over 7}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{21} \over {23}}...{{21} \over {27}}\)
c) \({7 \over 9}...{9 \over 7}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{95} \over {96}}...{{96} \over {95}}\)
2. a) Viết các phân số \({8 \over {11}};{8 \over 5};{8 \over 7}\) theo thứ tự từ bé đến lớn:
b) Viết các phân số \({{12} \over {10}};{{15} \over {25}};{{16} \over {20}}\) theo thứ tự lớn đến bé:
3. Viết phân số có tử số, mẫu số là số lẻ lớn hơn 6 và bé hơn 10.
a) Phân số đó bé hơn 1.
b) Phân số đó bằng 1.
c) Phân số đó lớn hơn 1.
4. Tính:
a) \({{5 \times 6 \times 7 \times 8} \over {6 \times 7 \times 8 \times 9}}\)
b) \({{42 \times 32} \over {12 \times 14 \times 16}}\)

1.
a) \({6 \over {11}}<{8 \over {11}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{9 \over {15}}={6 \over {10}}\)
b) \({8 \over 5}>{8 \over 7}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{21} \over {23}}>{{21} \over {27}}\)
c) \({7 \over 9}<{9 \over 7}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{95} \over {96}}<{{96} \over {95}}\)
2.
a) Theo thứ tự từ bé đến lớn: \({8 \over {11}};{8 \over 7};{8 \over 5}\)
b) Theo thứ tự từ lớn đến bé: \({{12} \over {10}};{{16} \over {20}};{{15} \over {25}}\)
Rút gọn các phân số trên ta được:
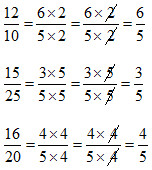
Ba phân số trên sau khi rút gọn thì có cùng mẫu số. Những phân số có cùng mẫu số, phân số nào có tử lớn hơn thì phân số đó lớn hơn.
Ta được: \({6 \over 5} > {4 \over 5} > {3 \over 5}\) nên \({{12} \over {10}} > {{16} \over {20}} > {{15} \over {25}}\)
3. Phân số có tử số, mẫu số là số lẻ lớn hơn 6 và bé hơn 10.
Vì phân số có tử số, mẫu só là số lẻ lớn hơn 6 nhỏ hơn 10. Vậy tử số đó có thể là 7 và 9
a) Phân số đó bé hơn 1. Vậy phân số đó là \({7 \over 9}\)
b) Phân số đó bằng 1. Vậy phân số đó là \({7 \over 7};{9 \over 9}\)
c) Phân số đó lớn hơn 1. Vậy phân số đó là \({9 \over 7}\)
4. Tính