a) Vẽ vào vở hình 12 trong đó ba điểm S, R, A thẳng hàng và \(\widehat {{\rm{AR}}M} = \widehat {S{\rm{R}}N} = {130^O}\)
b) Tính \(\widehat {{\rm{AR}}N},\widehat {M{\rm{RS}}},\widehat {M{\rm{R}}N}\)
c) Dùng thước đo góc kiểm tra lại kết quả.
Giải
a) Ta có hình vẽ
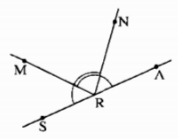
b) Vì \(\widehat {{\rm{AR}}N}\) và \(\widehat {S{\rm{RN}}}\) kề bù nên:
\(\widehat {{\rm{AR}}N} + \widehat {S{\rm{R}}N} = {180^O}\)
Thay \(\widehat {S{\rm{RN}}} = {130^O}\) ta có:
\(\widehat {{\rm{AR}}N} + {130^O} = {180^O}\)
\( \Rightarrow \widehat {{\rm{AR}}N} = {180^O} - {130^O} = {50^O}\)
Advertisements (Quảng cáo)
Vì \(\widehat {{\rm{AR}}M}\) và \(\widehat {M{\rm{RS}}}\) kề bù nên:
\(\widehat {{\rm{AR}}M} + \widehat {M{\rm{RS}}} = {180^O}\)
Thay \(\widehat {{\rm{AR}}M} = {130^O}\) ta có:
\({130^O} + \widehat {M{\rm{RS}}} = {180^O}\)
\( \Rightarrow \widehat {M{\rm{RS}}} = {180^O} - {130^O} = {50^O}\)
Vì hai tia RN và RM nằm trên cùng môt nửa mặt phẳng bờ chứa tia RA
\(\widehat {{\rm{AR}}N} = {50^O};\widehat {{\rm{AR}}M} = {130^O}\) suy ra \(\widehat {{\rm{AR}}N} < \widehat {{\rm{AR}}M}\)
Nên tia RN nằm giữa hai tia RA và RM
\(\Rightarrow \widehat {{\rm{AR}}N} + \widehat {M{\rm{R}}N} = \widehat {{\rm{AR}}M}\). Thay \(\widehat {{\rm{AR}}N} = {50^O};\widehat {{\rm{AR}}M} = {130^O}\) ta có:
$${50^O} + \widehat {M{\rm{R}}N} = {130^O}$$
\( \Rightarrow \widehat {M{\rm{R}}N} = {130^O} - {50^O} = {80^O}\)
