Bài 30 trang 75 SBT Toán lớp 7 Cánh diều: Ở Hình 17 có ba điểm A, B, C thẳng hàng; AD và BE vuông góc với AB; AD = BC...

Ở Hình 17 có ba điểm A, B, C thẳng hàng; AD và BE vuông góc với AB; AD = BC; DC = CE. Chứng minh:

a) ΔDAC = ΔCBE;

b) $\widehat {DCE} = 90^\circ$.

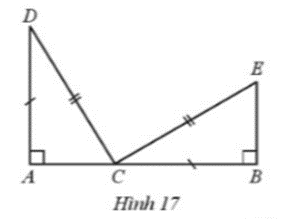
- Xét các điều kiện về cạnh để chứng minh hai tam giác vuông DAC và CDE bằng nhau trong trường hợp cạnh huyền – cạnh góc vuông.

- Từ ΔDAC = ΔCBE suy ra $\widehat D = \widehat {BCE}$. Tính được số đo góc BCE.

a) Xét ∆DAC và ∆CBE có:

$\widehat {CAD} = \widehat {EBC}$ (cùng bằng 90°),

CD = CE (giả thiết),

AD = BC (giả thiết).

Do đó ΔDAC = ΔCBE (cạnh huyền – cạnh góc vuông).

Vậy ΔDAC = ΔCBE.

b) Vì ΔDAC = ΔCBE (chứng minh câu a)

Suy ra $\widehat {DCA} = \widehat {CEB}$ (cặp góc tương ứng).

Xét ΔCEB vuông tại B có: $\widehat {CEB} + \widehat {ECB} = 90^\circ$ (trong tam giác vuông, tổng hai góc nhọn bằng 90°).

Suy ra $\widehat {DCA} + \widehat {ECB} = 90^\circ$

Mặt khác $\widehat {DCA} + \widehat {DCE} + \widehat {ECB} = 180^\circ$

Suy ra $\widehat {DCE} = 180^\circ  - \left( {\widehat {DCA} + \widehat {ECB}} \right) = 180^\circ  - 90^\circ  = 90^\circ$

Vậy $\widehat {DCE} = 90^\circ .$