Giải Bài 57 trang 86 sách bài tập toán 7 - Cánh diều - Bài 8: Đường vuông góc và đường xiên

Cho tam giác ABC vuông tại A, tia phân giác của góc B cắt AC ở D. So sánh độ dài AD và DC.

Chứng minh: AD = HD và HD < DC suy ra AD < DC

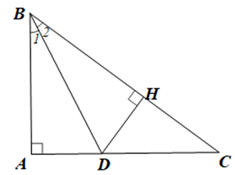
Kẻ DH ⊥ BC.
Vì BD là tia phân giác của góc ABC nên \({\hat B_1} = {\hat B_2}\)
Advertisements (Quảng cáo)
Xét ∆DAB và ∆DHB có:
\(\widehat {BAD} = \widehat {BHD}\left( { = 90^\circ } \right)\)
BD là cạnh chung,
\({\hat B_1} = {\hat B_2}\) (chứng minh trên)
Do đó ∆DAB = ∆DHB (cạnh huyền – góc nhọn).
Suy ra AD = HD (hai cạnh tương ứng) (1)
Vì ∆DHC vuông tại H nên HD < DC (trong tam giác vuông, cạnh huyển là cạnh lớn nhất) (2)
Từ (1) và (2) suy ra AD < DC.
Vậy AD < DC.
