
Cho tam giác ABC vuông tại A (AB < AC), BD là tia phân giác của góc ABC (D ∈ AC). Qua C kẻ tia Cx vuông góc với AC cắt BD tại M.
a) Chứng minh tam giác CBM là tam giác cân.
b) So sánh độ dài CM và AC.

- Chứng minh: \(\widehat M = \widehat {{B_2}}\) suy ra tam giác CBM cân tại C.
- Chứng minh: CM = BC và BC > AC suy ra CM > AC

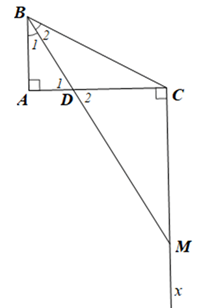
a) Vì ∆ABD vuông tại A nên \({\hat B_1} + {\hat D_1} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90o)
Advertisements (Quảng cáo)
Mà \({\hat B_1} = {\hat B_2}\) (do BD là tia phân giác của góc ABC) và \({\hat D_1} = {\hat D_2}\) (hai góc đối đỉnh).
Nên \({\hat B_2} + {\hat D_2} = 90^\circ \)
Vì ∆CDM vuông tại C nên \(\hat M + {\hat D_2} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90o).
Suy ra \(\hat M = {\hat B_2}\)
Do đó tam giác CBM cân tại C.
Vậy tam giác CBM cân tại C.
b) Vì tam giác CBM cân tại C (chứng minh câu a)
Nên CM = BC.
Vì ∆ABC vuông tại A nên BC > AC (trong tam giác vuông, cạnh huyển là cạnh lớn nhất).
Suy ra CM > AC.
Vậy CM > AC.
