
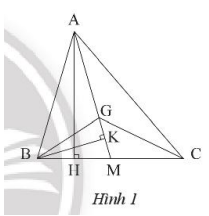
Cho tam giác ABC có trung tuyến AM và G là trọng tâm. Chứng minh:
|
a) \({S_{AMB}} = {S_{AMC}}\) |
b) \({S_{ABG}} = 2{S_{BMG}}\) |
c) \({S_{GAB}} = {S_{GBC}} = {S_{GAC}}\) |

So sánh đường cao và các cạnh đáy tương ứng của các tam giác

Advertisements (Quảng cáo)
a) Vẽ đường cao AH của tam giác ABC.
Hai tam giác AMB và AMC có cùng đường cao AH và có cạnh đáy bằng nhau: BM = CM
Suy ra: \({S_{AMB}} = {S_{AMC}}\)(vì \({S_{AMB}} = \frac{1}{2}.AH.BM{;^{}}{S_{AMC}} = \frac{1}{2}.AN.CM\))
b) Vẽ đường cao BK của tam giác BGM.
Hai tam giác ABG và BMG có cùng đường cao BK và có cạnh đáy AG = 2MG.
Suy ra: \({S_{ABG}} = \frac{1}{2}.BK.AG = \frac{1}{2}.BK.2MG = 2.\frac{1}{2}.BK.MG = 2{S_{BMG}}\)
c) Ta có:
\({S_{ABG}} = \frac{2}{3}{S_{ABM}} = \frac{1}{3}{S_{ABC}}\)
Tương tự: \({S_{ACG}} = \frac{2}{3}{S_{ACM}} = \frac{1}{3}{S_{ABC}}\)
Suy ra: \({S_{BCG}} = \frac{1}{3}{S_{ABC}}\)
Vậy: \({S_{GAB}} = {S_{GBC}} = {S_{GAC}} = \frac{1}{3}{S_{ABC}}\)
