
Quan sát Hình 8
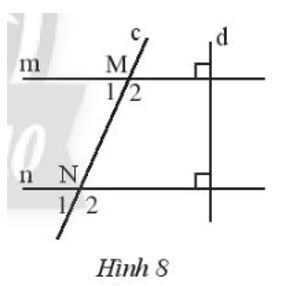
a) Chứng minh rằng m // n.
b) Cho \(\widehat {{N_2}}\) =70°. Tính \(\widehat {{M_1}}\), \(\widehat {{M_2}}\)

Ta sử dụng tính chất 2 góc đồng vị để tính được góc M2 và dùng tính chất 2 góc kề bù tính được N1 sau đó lại dùng tính chất 2 góc đồng vị tính được \(\widehat{M_1}\).
Advertisements (Quảng cáo)

a) Ta có m ⊥ d và n ⊥ d.
Do đó m // n (hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song).
Vậy m // n.
b) Vì m // n nên \(\widehat {{M_2}}\) = \(\widehat {{N_2}}\) =70° (hai góc đồng vị).
Mà \(\widehat {{M_2}}\) và \(\widehat {{M_1}}\) là hai góc kề bù nên:
\(\widehat {{M_1}}\) + \(\widehat {{M_2}}\) =180°
Suy ra \(\widehat {{M_1}}\) =180°− \(\widehat {{M_2}}\) =180°−70°=110°.
Vậy \(\widehat {{M_2}}\) =70° và \(\widehat {{M_1}}\) =110°
