
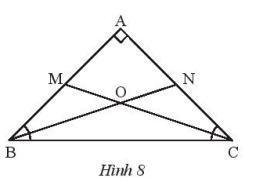
Cho tam giác ABC vuông cân tại A. Tia phân giác của góc B cắt AC tại N, tia phân giác của góc C cắt AB tại M. Gọi O là giao điểm của BN và CM.
a) Tính số đo các góc OBC, OCB.
b) Chứng minh rằng tam giác OBC cân.
c) Tính số đo góc BOC.

- Sử dụng tia phân giác của một góc để tính số đo góc.
Advertisements (Quảng cáo)
- Chứng minh \(\widehat {OBC} = \widehat {OCB}\) suy ra tam giác OBC cân tại O.
- Sử dụng định lí tổng ba góc trong một tam giác bằng \({180^o}\) để tính các góc còn lại của tam giác.

a) Vì tam giác ABC vuông cân tại A nên \(\widehat B = \widehat C = {45^o}\)
Ta có: \(\widehat {OBC} = \widehat {OCB} = \frac{{{{45}^o}}}{2} = 22,{5^o}\)
b) Tam giác OBC có \(\widehat {OBC} = \widehat {OCB}\) nên tam giác OBC cân tại O.
c) ta có: \(\widehat {BOC} = {180^o} - \left( {\widehat {OBC} + \widehat {OCB}} \right) = {180^o} - {45^o} = {135^o}\)
