
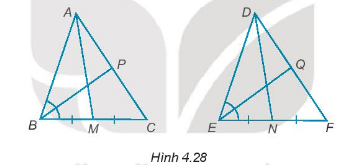
Cho tam giác ABC bằng tam giác DEF (h.4.28)
a) Gọi M và N lần lượt là trung điểm các đoạn thẳng BC và EF. Chứng minh rằng
AM = DN.
b) Trên hai cạnh AC và DF lấy 2 điểm P và Q sao cho BP, EQ lần lượt là phân giác của các góc ABC và DEF. Chứng minh rằng
BP = EQ.

a) Chứng minh 2 tam giác ABM và DEN bằng nhau.
b) Chứng minh 2 tam giác ABP và DEQ bằng nhau

Advertisements (Quảng cáo)
a)
Xét \(\Delta ABM\) và \(\Delta DEN\) có:
\(\begin{array}{l}AB = BE\left( do {\Delta ABC = \Delta DEF} \right)\\\widehat B = \widehat E\left( do{\Delta ABC = \Delta DEF} \right)\\BM = EN\left( {gt} \right)\end{array}\)
\(\Rightarrow \Delta ABM = \Delta DEN\left( {c - g - c} \right)\)
\(\Rightarrow AM = DN\) (2 cạnh tương ứng)
b)
Xét \(\Delta ABP\) và \(\Delta DEQ\) có:
\(\widehat {ABP} = \widehat {DEQ}\left( {\dfrac{1}{2}\widehat B = \dfrac{1}{2}\widehat E} \right)\)
\(\widehat A = \widehat D\left( {\Delta ABC = \Delta DEF} \right)\)
AB = DE (gt)
\( \Rightarrow \Delta ABP = \Delta DEQ\left( {g - c - g} \right)\)
\( \Rightarrow BP = EQ\) (2 cạnh tương ứng)
