Bài 4.34 trang 65 SBT Toán lớp 7 Kết nối tri thức: Cho hình vuông ABCD. Gọi M và N lần lượt là trung điểm của AB và AD (H.4.36). Chứng...

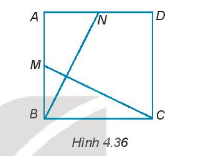
Cho hình vuông ABCD. Gọi M và N lần lượt là trung điểm của AB và AD (H.4.36). Chứng minh rằng $BN = CM;BN \bot CM.$

-Chứng minh $\Delta BMC = \Delta ANB\left( {c - g - c} \right)$

-Gọi E là giao điểm của BN và CM.

-Chứng minh $\widehat {BEM} = \widehat {NAB} = {90^0}$. 

Xét $\Delta BMC$ và $\Delta ANB$ có:

$BC = AB\\BM = AN\\\widehat B = \widehat A = {90^0}\\ \Rightarrow \Delta BMC = \Delta ANB\left( {c - g - c} \right)$

$\Rightarrow MC = NB$ (2 cạnh tương ứng)

Gọi E là giao điểm của BN và CM.

Vì $\Delta BMC = \Delta ANB\left( {cmt} \right)$

$\Rightarrow \widehat {CMB} = \widehat {BNA}; \widehat {BCM} = \widehat {ABN}$ (2 góc tương ứng) (1)

Theo định lí tổng ba góc trong tam giác, ta có:

$\widehat {BEM}+ \widehat {EMB} + \widehat {EBM}=180^0 (2)\\\widehat {NAB}+\widehat {BNA}+\widehat {NBA}=180^0$(3)

Từ (1), (2) và (3) $\Rightarrow \widehat {BEM} = \widehat {NAB}$

Mà $\widehat {NAB} = {90^0}$

$\Rightarrow \widehat {BEM} = {90^0}\\ \Rightarrow BN \bot CM$